Chapitre 10 Étape 2. Coder le modèle
Traduisons notre modèle…
\[PT_{ijk} \sim Longueur_i + Lac_j + Espèce_k + \varepsilon_{ijk}\]
… en code R
lmer(Z_TP ~ Z_Length + (1 | Lake) + (1 | Fish_Species), data = fish.data,
REML = TRUE)## Linear mixed model fit by REML ['lmerMod']
## Formula: Z_TP ~ Z_Length + (1 | Lake) + (1 | Fish_Species)
## Data: fish.data
## REML criterion at convergence: 72.4662
## Random effects:
## Groups Name Std.Dev.
## Lake (Intercept) 0.4516
## Fish_Species (Intercept) 0.9301
## Residual 0.2605
## Number of obs: 180, groups: Lake, 6; Fish_Species, 3
## Fixed Effects:
## (Intercept) Z_Length
## 9.752e-14 4.198e-01Où:
lmer()est la fonction “linear mixed model” du packagelme4(1 | Lake)indique que les ordonnées à l’origine peuvent varier entre les lacsREML = TRUEspécifie la méthode d’estimation
10.1 Note sur les méthodes d’estimation
REML (Restricted Maximum Likelihood) est la méthode par défaut dans la fonction lmer (voir ?lmer).
La méthode de maximum de vraisemblance (ML, pour Maximum Likelihood) sous-estime les variances du modèle par un facteur \((n-k) / n\), ou \(k\) est le nombre d’effes fixes.
Les estimations REML peuvent être utilisées lorsque vous comparez des modèles ayant les mêmes effets fixes (c’est-à-dire des modèles imbriqués). Cependant, si vous comparez des modèles où les effets fixes diffèrent d’un modèle à l’autre, il est préférable d’utiliser le maximum de vraisemblance pour ajuster les paramètres car cette méthode ne dépend pas des coefficients des effets fixes. L’ajustement en utilisant le maximum de vraisemblance est fait en mettant REML=FALSE dans la commande lmer.
Consultez cet article pour plus d’information sur la différence entre ML et REML.
En résumé:
REML pour comparer des modèles avec des effets aléatoires nichés et la même structure d’effets fixes
ML pour comparer des modèles avec des effets fixes nichés et la même structure d’effets aléatoires
ML pour comparer des modèles avec et sans effets aléatoires
10.2 Différentes structures de modèles
Comment faire si on souhaite que la pente puisse varier?
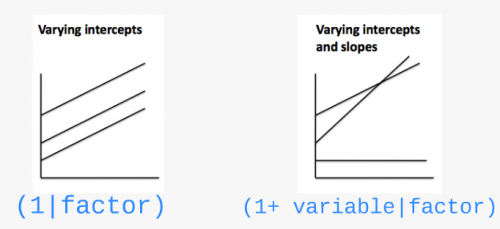
Il y a différentes structures possibles pour le modèle:
(1 | Lake)effet aléatoire par lac à l’ordonnée à l’origine(1 + Z_Length | Lake)effet aléatoire par lac à l’ordonnée à l’origine et la pente en réponse à la longueur corporelle (NB: (Z_Length | Lake)donne le même résultat)(-1 + Z_Length | Lake)pour avoir uniquement l’effet aléatoire sur la pente(1 | Lake) + (1 | Species)pour des effets aléatoires croisés(1 | Lake:Fish_Species)pour utiliser l’interaction entre 2 facteurs groupantSi votre jeu de données inclus des effets nichés, vous pouvez utiliser
/pour les déclarer, e.g.(1 | facteur1 / facteur2)sifacteur2est niché dansfacteur1(voir stack-exchange)
10.3 Défi 4
Réécrivez le code suivant de façon à ce que les pentes de la relation position trophique en fonction de longueur corporelle varient par lac et par espèces:
# Défi 4: Réécrivez le code suivant de façon à ce que les
# **pentes** de la relation position trophique en fonction
# de longueur corporelle **varient par lac et par
# espèces**:
lmer(Z_TP ~ Z_Length + (1 | Lake) + (1 | Fish_Species), data = fish.data,
REML = TRUE)## Linear mixed model fit by REML ['lmerMod']
## Formula: Z_TP ~ Z_Length + (1 | Lake) + (1 | Fish_Species)
## Data: fish.data
## REML criterion at convergence: 72.4662
## Random effects:
## Groups Name Std.Dev.
## Lake (Intercept) 0.4516
## Fish_Species (Intercept) 0.9301
## Residual 0.2605
## Number of obs: 180, groups: Lake, 6; Fish_Species, 3
## Fixed Effects:
## (Intercept) Z_Length
## 9.752e-14 4.198e-01Défi 4 Solution:
# Défi 4 Solution:
lmer(Z_TP ~ Z_Length + (1 + Z_Length | Lake) + (1 + Z_Length |
Fish_Species), data = fish.data, REML = TRUE)## boundary (singular) fit: see help('isSingular')## Linear mixed model fit by REML ['lmerMod']
## Formula:
## Z_TP ~ Z_Length + (1 + Z_Length | Lake) + (1 + Z_Length | Fish_Species)
## Data: fish.data
## REML criterion at convergence: 20.5786
## Random effects:
## Groups Name Std.Dev. Corr
## Lake (Intercept) 0.45279
## Z_Length 0.02378 -0.82
## Fish_Species (Intercept) 0.93103
## Z_Length 0.15728 1.00
## Residual 0.22341
## Number of obs: 180, groups: Lake, 6; Fish_Species, 3
## Fixed Effects:
## (Intercept) Z_Length
## -0.0009025 0.4223738
## optimizer (nloptwrap) convergence code: 0 (OK) ; 0 optimizer warnings; 1 lme4 warnings10.4 Défi 5
Pour déterminer si vous avez construit le meilleur modèle mixte sur la base de vos connaissances préalables, vous devez comparer ce modèle a priori à d’autres modèles alternatifs.
Avec l’ensemble de données sur lequel vous travaillez, il existe plusieurs modèles alternatifs qui pourraient mieux s’adapter à vos données. Pour le défi 5, faites une liste de 7 modèles alternatifs qui pourraient être comparés à celui-ci:
# Défi 5 : Faites une liste de 7 modèles alternatifs qui
# pourraient être comparés à ce modèle initial:
lmer(Z_TP ~ Z_Length + (1 | Lake) + (1 | Fish_Species), data = fish.data,
REML = TRUE)## Linear mixed model fit by REML ['lmerMod']
## Formula: Z_TP ~ Z_Length + (1 | Lake) + (1 | Fish_Species)
## Data: fish.data
## REML criterion at convergence: 72.4662
## Random effects:
## Groups Name Std.Dev.
## Lake (Intercept) 0.4516
## Fish_Species (Intercept) 0.9301
## Residual 0.2605
## Number of obs: 180, groups: Lake, 6; Fish_Species, 3
## Fixed Effects:
## (Intercept) Z_Length
## 9.752e-14 4.198e-01Notez: Si nous avions différents effets fixes entre les modèles ou un modèle sans effects aléatoires, nous aurions dû indiquer REML = FALSE pour les comparer avec une méthode de vraisemblance comme l’AIC.
Défi 5 Solution:
Nous allons aussi construire le modèle linéaire de base lm() parce qu’il est toujours utile de voir la variation dans les valeurs de AICc.
# Solution du défi 5: Modèle linéaire de base
M0 <- lm(Z_TP ~ Z_Length, data = fish.data)A fin de comparer ce modèle aux LMMs, il est important de changer la méthode d’estimation en ML (REML=FALSE) pour tous les autres modèles car lm() n’utilise pas la même méthode d’estimation que lmer().
Examinons les autres modèles que vous auriez pu écrire (notez REML = FALSE):
# Solution du défi 5, autres modèles potentiels Notez que
# REML = FALSE afin de comparer avec le modèle linéaire de
# base où la méthode d'estimation = ML.
# Modele linéaire de base
M0 <- lm(Z_TP ~ Z_Length, data = fish.data)
# modèle complet avec variation des ordonnées à l'origine
M1 <- lmer(Z_TP ~ Z_Length + (1 | Fish_Species) + (1 | Lake),
data = fish.data, REML = FALSE)
# modèle complet avec variation des ordonnées à l'origine
# et de pentes
M2 <- lmer(Z_TP ~ Z_Length + (1 + Z_Length | Fish_Species) +
(1 + Z_Length | Lake), data = fish.data, REML = FALSE)## boundary (singular) fit: see help('isSingular')# Pas d'effet lac, les ordonnées à l'origine varient par
# espèces
M3 <- lmer(Z_TP ~ Z_Length + (1 | Fish_Species), data = fish.data,
REML = FALSE)
# Pas d'effet espèces, les ordonnées à l'origine varient
# par lac
M4 <- lmer(Z_TP ~ Z_Length + (1 | Lake), data = fish.data, REML = FALSE)
# Pas d'effet de lac, les ordonnées à l'origine et les
# pentes varient par espèces
M5 <- lmer(Z_TP ~ Z_Length + (1 + Z_Length | Fish_Species), data = fish.data,
REML = FALSE)## boundary (singular) fit: see help('isSingular')# Pas d'effet de l'espèces, les ordonnées à l'origine et
# les pentes varient par lac
M6 <- lmer(Z_TP ~ Z_Length + (1 + Z_Length | Lake), data = fish.data,
REML = FALSE)## boundary (singular) fit: see help('isSingular')# modèle complet, variation d'ordonnée à l'origine et pente
# par lac
M7 <- lmer(Z_TP ~ Z_Length + (1 | Fish_Species) + (1 + Z_Length |
Lake), data = fish.data, REML = FALSE)## boundary (singular) fit: see help('isSingular')# modèle complet, variation d'ordonnée à l'origine et pente
# par espèces
M8 <- lmer(Z_TP ~ Z_Length + (1 + Z_Length | Fish_Species) +
(1 | Lake), data = fish.data, REML = FALSE)## boundary (singular) fit: see help('isSingular')Lorsqu’on ajuste des MLM avec lmer(), il est possible de faire face à certaines erreurs our avertissements comme:
boundary (singular) fit: see ?isSingular, voir cette discussionModel failed to converge with max|grad| ..., voir cette discussion
Voici une liste de problèmes possibles et comment les résoudre.
10.5 Comparing models
Maintenant que nous avons une liste de modèles potentiels, nous voulons les comparer entre eux pour sélectionner celui(ceux) qui a(ont) le plus de pouvoir prédictif.
Les modèles peuvent être comparés en utilisant la fonction AICc provenant du package MuMIn. Le critère d’information Akaike (AIC) est une mesure de qualité du modèle pouvant être utilisée pour comparer les modèles.
AICc corrige pour le biais créé par les faibles tailles d’échantillon.
Pour trouver la valeur AICc d’un modèle, utilisez:
# Trouver la valeur AICc pour notre premier modèle (Modèle
# linéaire de base) avec le paquet MuMIn
MuMIn::AICc(M1)## [1] 77.30499Pour regrouper toutes les valeurs de l’AICc dans un seul tableau, utilisez MuMIn::model.sel() pour calculer l’AICc pour chaque modèle (avec d’autres sorties) et ensuite sélectionnez seulement les colonnes d’intérêt pour les imprimer dans un tableau.
# Pour regrouper toutes les valeurs de l'AICc dans un seul
# tableau, utilisez `MuMIn::model.sel()` pour calculer
# l'AICc pour chaque modèle (avec d'autres sorties) et
# ensuite sélectionnez seulement les colonnes d'intérêt
# pour les imprimer dans un tableau.
AIC.table <- MuMIn::model.sel(M0, M1, M2, M3, M4, M5, M6, M7,
M8)
# `df` est le degré de liberté `logLik` est le log de la
# vraisemblance `delta` est la différence d'AICc avec la
# valeur la plus petite
(AIC.table <- AIC.table[, c("df", "logLik", "AICc", "delta")])## df logLik AICc delta
## M8 7 -8.597929 31.84702 0.000000
## M2 9 -8.216019 35.49086 3.643839
## M1 5 -33.480080 77.30499 45.457965
## M7 7 -33.186374 81.02391 49.176890
## M5 6 -128.310995 269.10754 237.260517
## M3 4 -134.532965 277.29450 245.447480
## M4 4 -224.715763 457.66010 425.813076
## M6 6 -224.671201 461.82795 429.980930
## M0 3 -236.861362 479.85909 448.012065# Pour plus d'informations sur les autres sorties ou
# résultats de la fonction model.sel(), roulez
# `?model.sel`.Où:
dfmontre les degrés de libertélogLikest le log de la vraisemblancedeltaest la différence d’AICc avec la valeur la plus petite
Nous avons seulement affiché une partie des résultats retourné par la fonction model.sel(), voir ?model.sel pour plus d’informations.
Que signifient ces valeurs d’AICc?
- Le modèle avec le plus petit AICc a le plus grand pouvoir prédictif.
- Souvent on considère que deux modèles à +/- 2 unités d’AICc de différence ont un pouvoir prédictif équivalent.
- Examinons de plus proche M8 and M2. On peut exclure les autres modèles, car ils ont des AICc beaucoup plus élevés.
Notez qu’on utilise maintenant REML (i.e. REML=TRUE) puisqu’on compare deux modèles avec des effets aléatoires nichés et avec la même structure d’effets fixes.
# Examinons de plus proche M8 and M2 (les autres modèlesont
# des AICc beaucoup plus élevés) `REML = TRUE` parce qu'on
# compare deux modèles avec des effets aléatoires nichés et
# avec la même structure d'effets fixes
M8 <- lmer(Z_TP ~ Z_Length + (1 + Z_Length | Fish_Species) +
(1 | Lake), data = fish.data, REML = TRUE)## boundary (singular) fit: see help('isSingular')M2 <- lmer(Z_TP ~ Z_Length + (1 + Z_Length | Fish_Species) +
(1 + Z_Length | Lake), data = fish.data, REML = TRUE)## boundary (singular) fit: see help('isSingular')# Sortonz un tableau pour comparer M2 et M8
MuMIn::model.sel(M2, M8)[, c("df", "logLik", "AICc", "delta")]## df logLik AICc delta
## M8 7 -10.84011 36.33137 0.000000
## M2 9 -10.28932 39.63747 3.306098Le modèle M8 semble être le meilleur modèle parmi ceux qu’on a testé!
Quelle est la structure du meilleur modèle?
# Regardons à nouveau le meilleur modèle, quelle est sa
# structure?
M8 <- lmer(Z_TP ~ Z_Length + (1 + Z_Length | Fish_Species) +
(1 | Lake), data = fish.data, REML = FALSE)## boundary (singular) fit: see help('isSingular')# L'ordonnée à l'origine et l'effet de la longueur sur la
# position trophique peut varier selon l'espèce de
# poissons, mais seulement l'ordonnée à l'origine peut
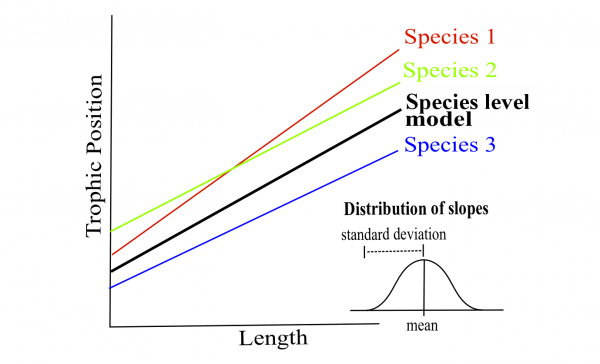
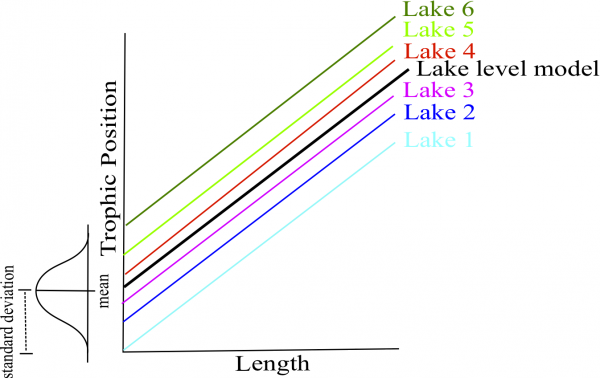
# varier par lacL’ordonnée à l’origine et l’effet de la longueur sur la position trophique peut varier selon l’espèce de poissons, mais seulement l’ordonnée à l’origine peut varier par lac.
Une fois que le meilleur modèle est sélectionné, il faut remettre la méthode d’estimation a REML = TRUE.
# Une fois que le meilleur modèle est sélectionné il faut
# remettre la méthode d'estimation a `REML = TRUE`
M8 <- lmer(Z_TP ~ Z_Length + (1 + Z_Length | Fish_Species) +
(1 | Lake), data = fish.data, REML = TRUE)## boundary (singular) fit: see help('isSingular')