Chapitre 14 Choisir la distribution des erreurs

Nous devons maintenant choisir une distribution d’erreurs. Ce choix sera informé par la structure de nos données.

La variable réponse constitue des données d’abondance, donc nous devons choisir une distribution de Poisson (i.e variance égale à la moyenne)

Jetons-y un coup d’oeil:

# Avant d'aller plus loin, nous devons choisir une
# distribution d'erreurs. Ce choix sera guidé par la
# structure de nos données.  Notre variable de réponse est
# une donnée de comptage, ce qui suggère que nous avons
# besoin d'une distribution de Poisson (c'est-à-dire que la
# variance est égale à la moyenne).
hist(dat.tf$total.fruits, breaks = 50, col = "blue", main = "",
    xlab = "Total fruits", ylab = "Count")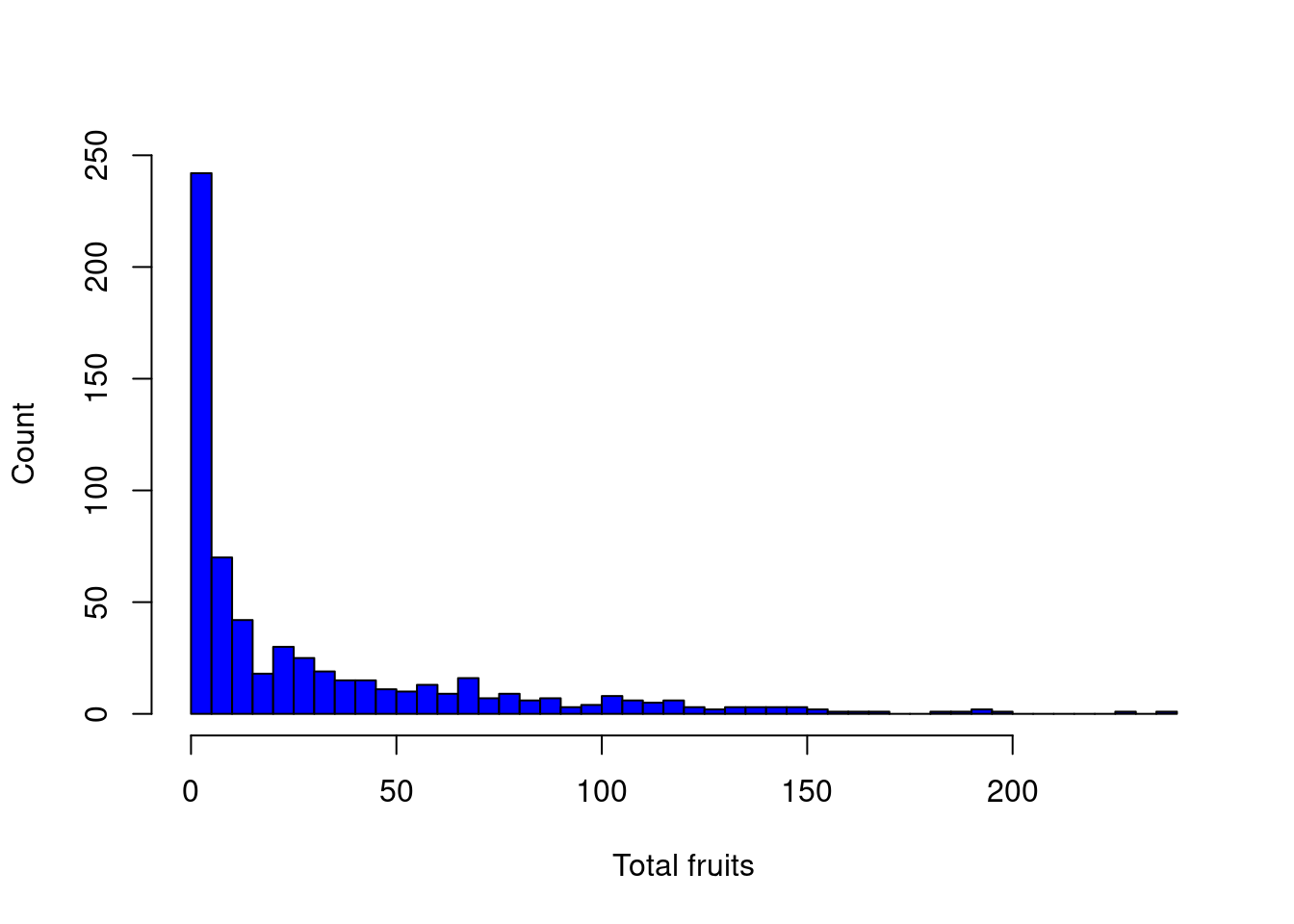

Cependant, comme nous le verrons, la variance de chaque groupe augmente beaucoup plus rapidement que prévu…

Exploration de la variance

Examinons de plus près la variance au sein de nos données.

Pour illustrer l’hétérogénéité de la variance, nous allons créer des boxplots du log du nombre total de fruits (variable réponse) par rapport aux différents facteurs environnementaux.

Créons d’abord de nouvelles variables qui représentent toutes les combinaisons de nutriments x herbivorie x facteur aléatoire.

# Explorons la variance dans nos données Créez de nouvelles
# variables qui représentent chaque combinaison de
# variables.
dat.tf <- within(dat.tf, {
    # genotype x nutrient x clipping
    gna <- interaction(gen, nutrient, amd)
    gna <- reorder(gna, total.fruits, mean)

    # population x nutrient x clipping
    pna <- interaction(popu, nutrient, amd)
    pna <- reorder(pna, total.fruits, mean)
})

Maintenant, visualisons:

# Boxplot of total fruits vs genotype x nutrient x clipping interaction
ggplot(data = dat.tf, 
       aes(factor(x = gna), y = log(total.fruits + 1))) +
  geom_boxplot(colour = "skyblue2", 
               outlier.shape = 21,
               outlier.colour = "skyblue2") +
  ylab("log (Total fruits)\n") + # \n creates a space after the title
  xlab("\nGenotype x nutrient x clipping") + # space before the title
  theme_bw() + theme(axis.text.x = element_blank()) +
  stat_summary(fun = mean, geom = "point", colour = "red")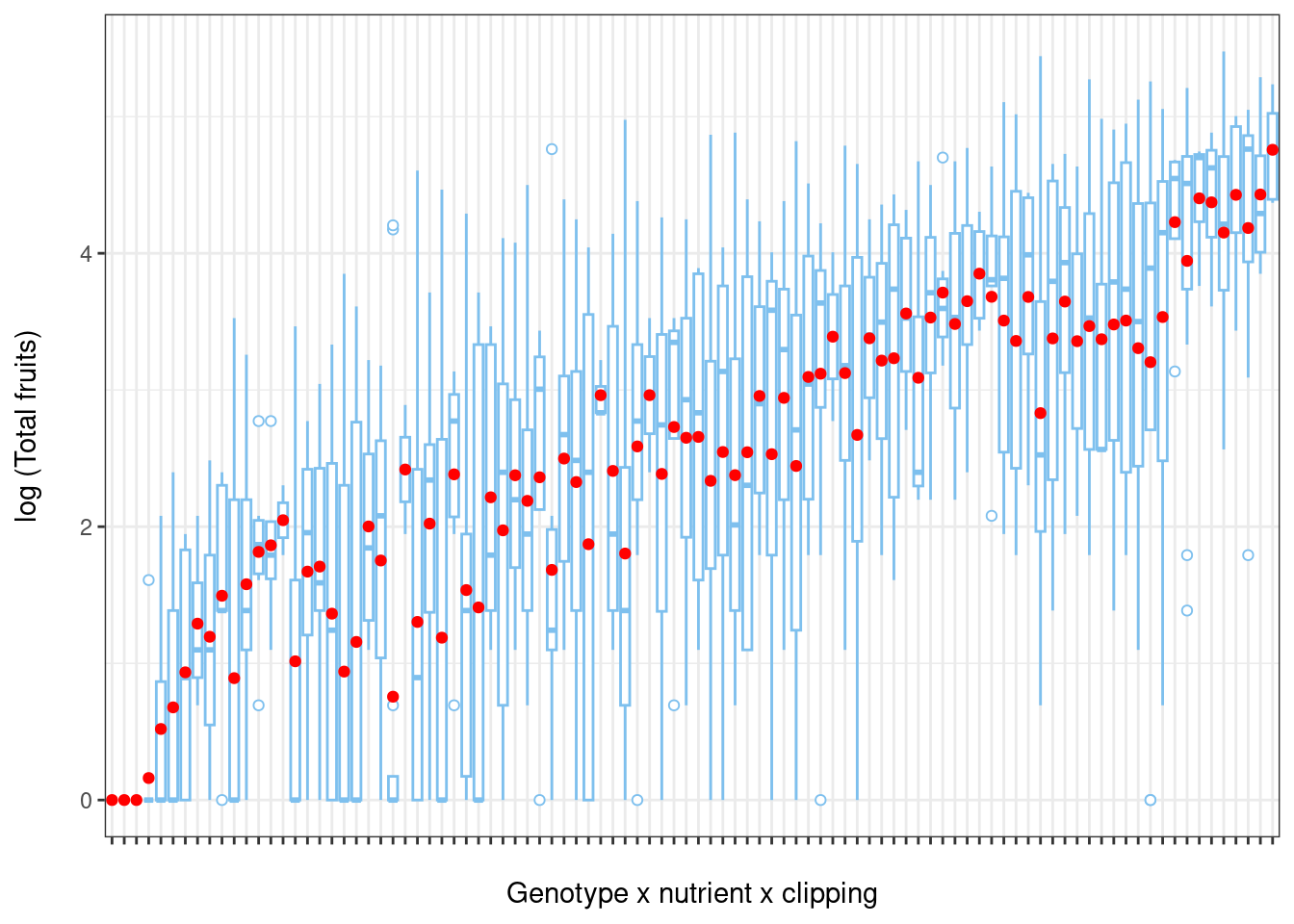

De même, la variance du total de fruits montre une grande hétérogénéité entre les populations (population x nutriments x herbivorie).

Retour au choix de la distribution des erreurs

Comme nous venons de voir, il existe une importante hétérogénéité parmi la variance de chaque groupe, même lorsque la variable réponse est transformée (i.e. log).

Pour identifier la famille de distribution la plus appropriée, nous pouvons examiner un graphique de diagnostic de la variance de chaque groupe par rapport à leurs moyennes. Nous présentons un exemple ci-dessous pour le regroupement par génotype x nutriments x herbivore (clipping).

1. Si nous observons une relation linéaire entre la variance et la moyenne avec une pente = 1, une famille de Poisson serait appropriée,
1. Si nous observons une relation moyenne-variance linéaire avec une pente> 1 (c. \(Var = \varphi\mu\) où \(\varphi > 1\)), la famille quasi-Poisson (tel que présenté ci-dessus) doit être utilisée,
1. Enfin, une relation quadratique entre la variance et la moyenne (c. \(Var = \mu(1+\alpha) or \mu(1+\mu/k)\)), est caractéristique des données surdispersées résultant d’une hétérogénéité sous-jacente entre les échantillons. Dans ce cas, la distribution binomiale négative (Poisson-gamma) serait plus appropriée.

# Figure diagnostique de variances par groupe vs moyennes
# par groupe (genotype x nutrient x clipping grouping).
# Code pour créer la figure:
# https://github.com/QCBSRworkshops/workshop07/blob/main/pres-fr/data/glmm_e.r

# On remarque beaucoup de variation entre les variances des
# échantillons dans les données transformées Par exemple,
# entre génotypes:
grpVars <- tapply(dat.tf$total.fruits, dat.tf$gna, var)

grpMeans <- tapply(dat.tf$total.fruits, dat.tf$gna, mean)

# Quasi-Poisson
lm1 <- lm(grpVars ~ grpMeans - 1)
phi.fit <- coef(lm1)
# Le -1 specifie un modèle avec une ordonnée à l'origine de
# 0

# Binomiale négative
lm2 <- lm(grpVars ~ I(grpMeans^2) + offset(grpMeans) - 1)
k.fit <- 1/coef(lm2)
# offset() spécifie qu'on veut ajouter un terme pour les
# moyennes de groupes avec un coefficient fixé à 1

# Non-parametric loess fit
Lfit <- loess(grpVars ~ grpMeans)

# La figure
plot(grpVars ~ grpMeans, xlab = "Group means", ylab = "Group variances")
abline(a = 0, b = 1, lty = 2)
text(105, 500, "Poisson")
curve(phi.fit * x, col = 2, add = TRUE)
# bquote() remplace des valeurs numériques dans des
# équations avec des symboles
text(110, 3900, bquote(paste("QP: ", sigma^2 == .(round(phi.fit,
    1)) * mu)), col = 2)
curve(x * (1 + x/k.fit), col = 4, add = TRUE)
text(104, 7200, paste("NB: k = ", round(k.fit, 1), sep = ""),
    col = 4)
mvec <- 0:120
lines(mvec, predict(Lfit, mvec), col = 5)
text(118, 2000, "loess", col = 5)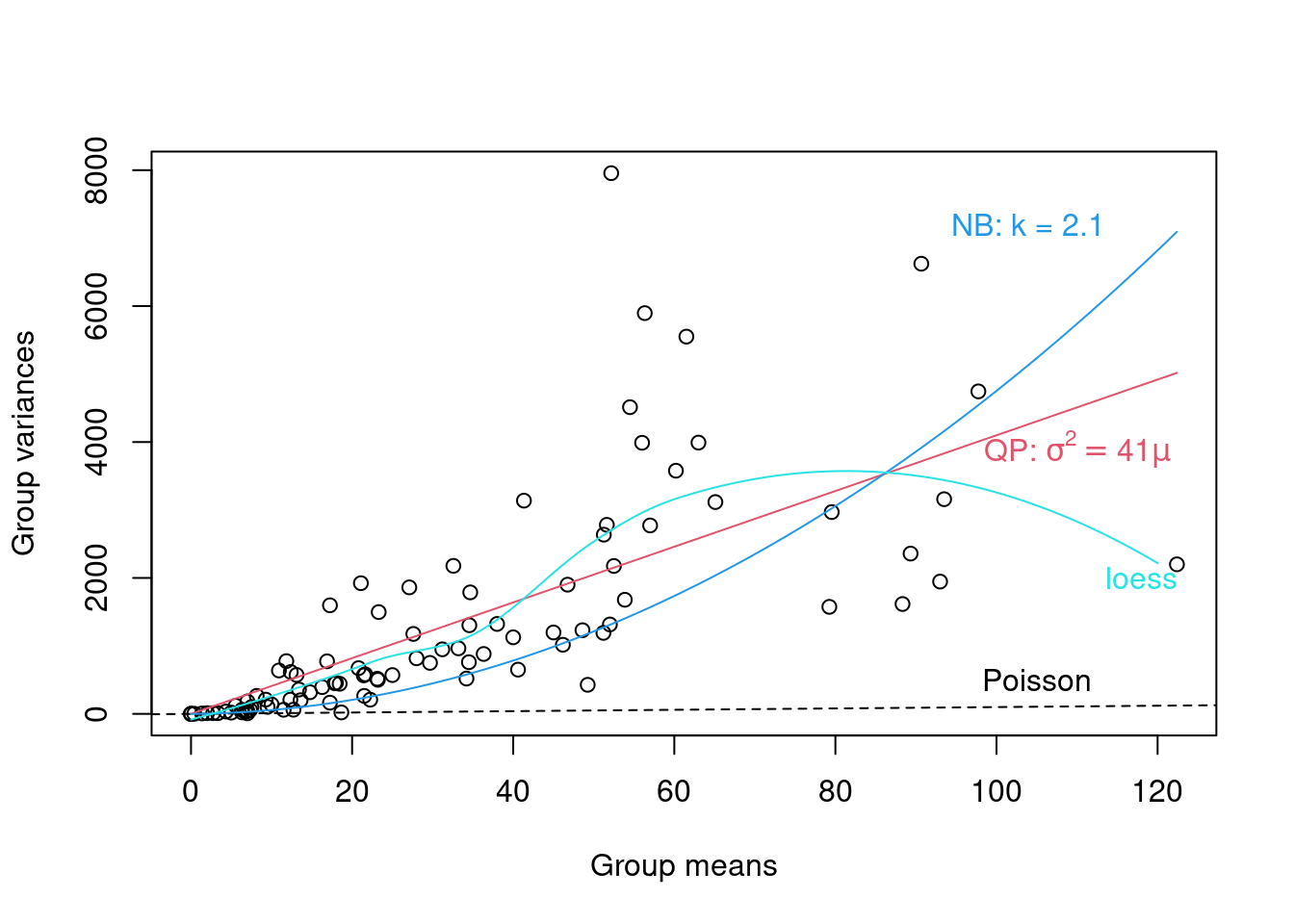

La figure ci-dessus montre qu’un modèle linéaire quasi-Poisson sera peut-être mieux qu’une binomiale négative, mais il faudrait continuer le processus de modélisation.