Chapitre 11 Step 3. Validation du modèle

Maintenant qu’on a trouvé notre modèle, on doit vérifier que le modèle respecte toutes les suppositions de base. Il faut donc:

1. Vérifier l’homogénéité de la variance:

Faire un graphique des valeurs prédites en fonction des valeurs résiduelles

2. Vérifier l’indépendance des résidus:

Graphique des résidus vs chaque covariable du modèle
Graphique des résidus vs chaque covariable non incluse du modèle

3. Vérifier la normalité:

Histogramme des résidus

11.1 1. Vérifier l’homogénéité de la variance

Afin de vérifier l’homogénéité de la variance, nous pouvons tracer les valeurs prédites par rapport aux valeurs résiduelles.

Une dispersion homogène des résidus signifie que l’hypothèse est respectée.

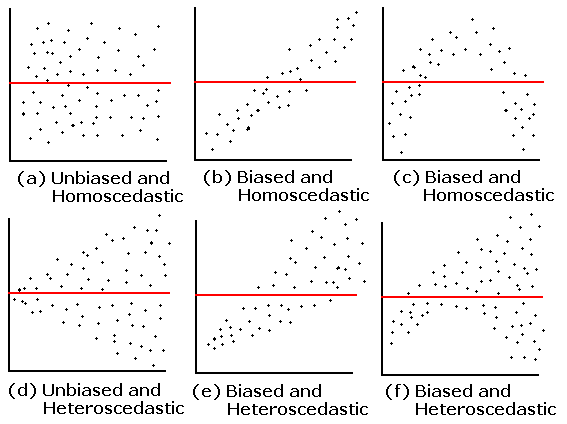
Maintenant, regardons nos données, la dispersion est-elle homogène ?

# Plotez les valeurs prédites par rapport aux valeurs
# résiduelles
par(mar = c(4, 4, 0.5, 0.5))
plot(resid(M8) ~ fitted(M8), xlab = "Predicted values", ylab = "Normalized residuals")
abline(h = 0, lty = 2)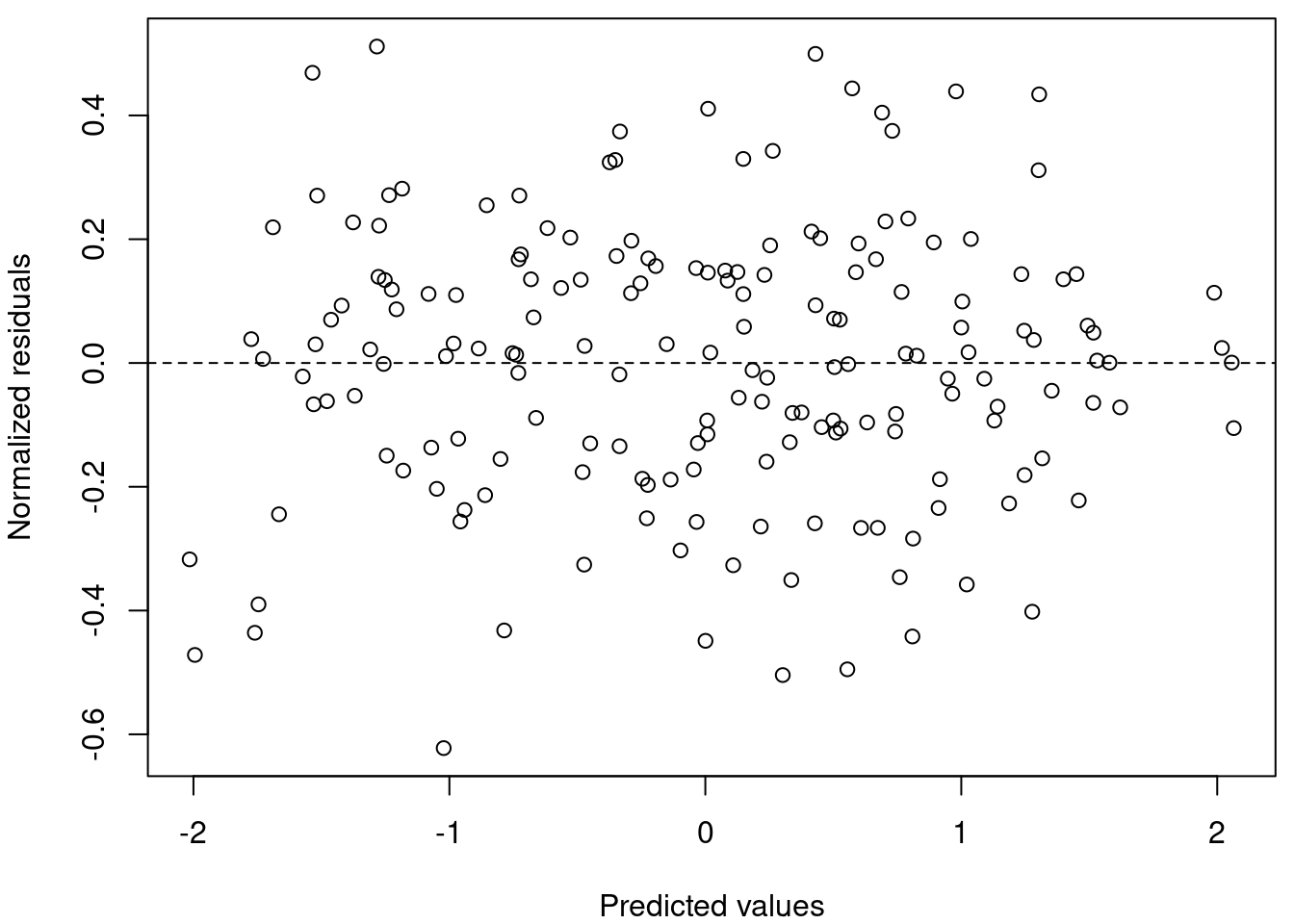

# La dispersion homogène des résidus signifie que
# l'hypothèse est respectée.

Oui! La dispersion homogène des résidus signifie que l’hypothèse est respectée.

11.2 2. Vérifier l’indépendance des résidus

Afin de vérifier l’indépendance des résidus du modèle par rapport à chaque covariable, nous allons (1) tracer les résidus par rapport à chaque covariable du modèle et (2) tracer les résidus par rapport à chaque covariable non incluse dans le modèle.

Commençons par (1) tracer les résidus par rapport à chaque covariable du modèle.

# Afin de vérifier l'indépendance des résidus du modèle,
# nous devons tracer les résidus en fonction de chaque
# covariable du modèle.
par(mfrow = c(1, 3), mar = c(4, 4, 0.5, 0.5))

plot(resid(M8) ~ fish.data$Z_Length, xlab = "Length", ylab = "Normalized residuals")
abline(h = 0, lty = 2)

boxplot(resid(M8) ~ Fish_Species, data = fish.data, xlab = "Species",
    ylab = "Normalized residuals")
abline(h = 0, lty = 2)

boxplot(resid(M8) ~ Lake, data = fish.data, xlab = "Lakes", ylab = "Normalized residuals")
abline(h = 0, lty = 2)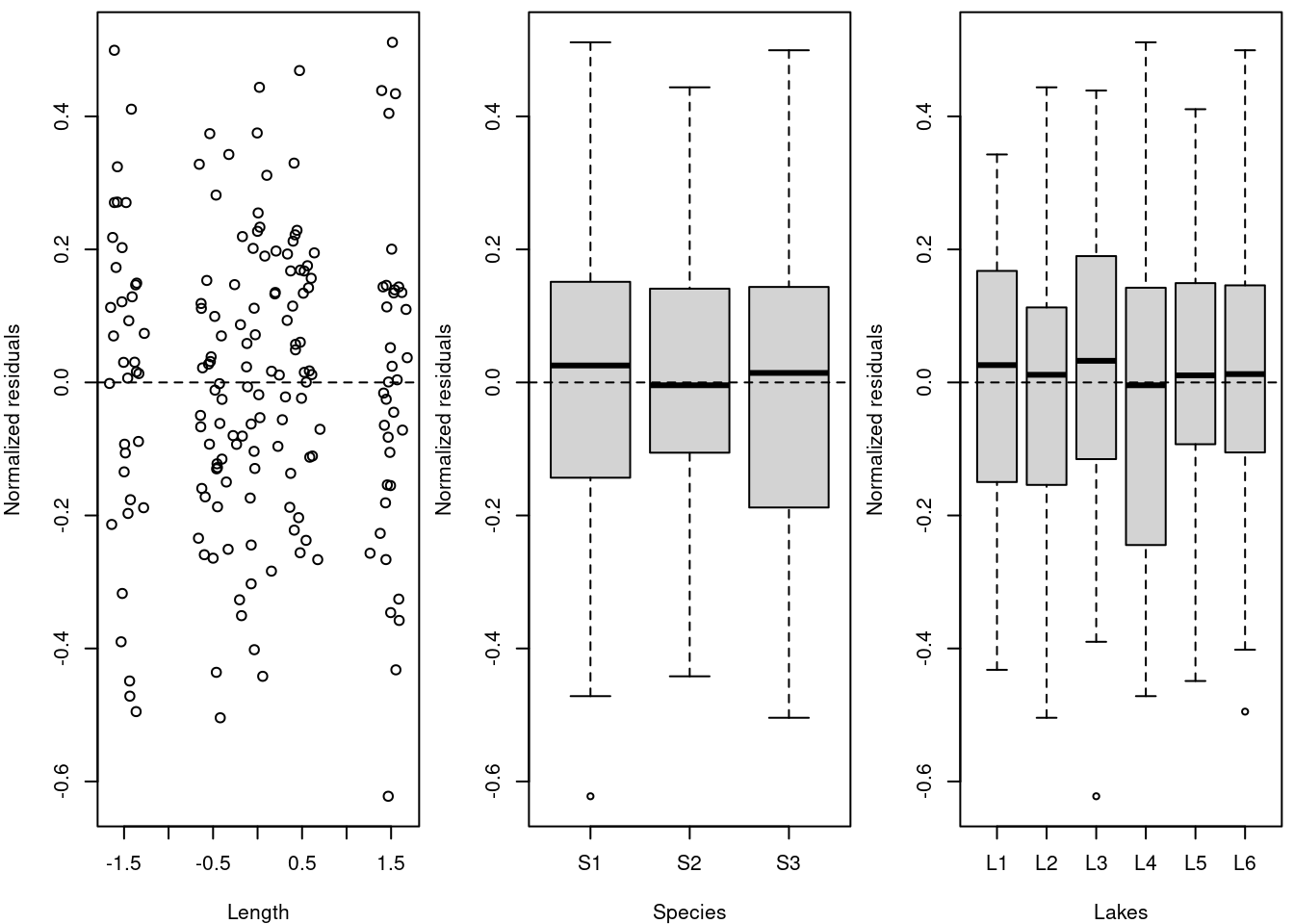

# La dispersion homogène des résidus autour de 0 signifie
# qu'il n'y a pas de modèle de résidus en fonction de la
# variable, donc l'hypothèse est respectée !  Note : Les
# groupes sont dus à la structure des données, où les
# poissons de seulement 5 classes de taille (grande,
# petite, et trois groupes intermédiaires) ont été
# capturés.

La dispersion homogène des résidus autour de 0 signifie qu’il n’y a pas de modèle de résidus en fonction de la variable, donc l’hypothèse est respectée!

*Remarque : les groupes sont dus à la structure des données, où les poissons de seulement 5 classes de taille (grande, petite, et trois groupes intermédiaires) ont été capturés.

Maintenant, nous devons (2) tracer les résidus par rapport à chaque covariable non incluse dans le modèle.

Si vous observez des tendances dans ces graphiques, vous saurez qu’il existe une variation dans votre ensemble de données qui pourrait être expliquée par ces covariables et vous devriez envisager de les inclure dans votre modèle. Cependant, comme nous avons inclus toutes les variables mesurées dans notre modèle, nous ne pouvons pas effectuer cette étape avec nos données.

11.3 3. Vérifier la normalité

Nous allons maintenant vérifier la normalité des résidus du modèle, car des résidus suivant une distribution normale indiquent que le modèle n’est pas biaisé.

# Vérifiez la normalité des résidus du modèle car des
# résidus suivant une distribution normale indiquent que le
# modèle n'est pas biaisé.
hist(resid(M8))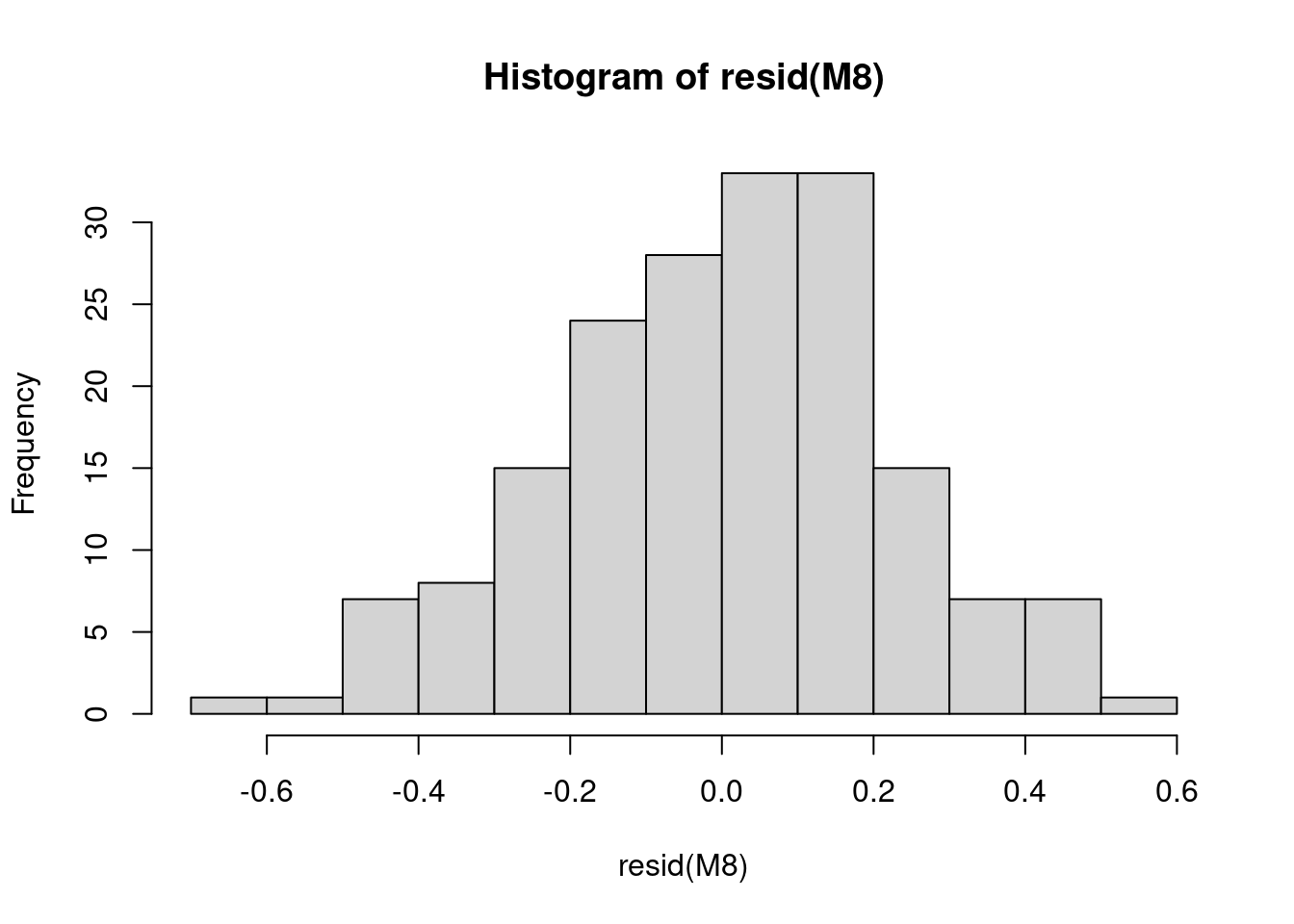

# Les résidus sont normaux ! Cela signifie que notre modèle
# n'est pas biaisé.

Les résidus sont normaux ! Cela signifie que notre modèle n’est pas biaisé.