Chapitre 11 Intro rapide aux modèles additifs généralisés à effets mixtes (GAMMs)

Lorsque les observations ne sont pas indépendantes, les GAMs peuvent être utilisés soit pour incorporer:

une structure de corrélation pour modéliser les résidus autocorrélés, comme:
le modèle autorégressif (AR, en anglais autoregressive);
le modèle avec moyenne mobile (MA, en anglais moving average); ou,
une combinaison des deux modèles (ARMA, en anglais, autoregressive moving average).
des effets aléatoires qui modélisent l’indépendance entre les observations d’un même site.

En plus de changer la fonction de base, nous pouvons aussi complexifier le modèle en intégrant une structure d’auto-corrélation (ou même des effets mixtes) en utilisant les fonctions gamm() dans la librairie mgcv. Bien que nous ne l’utilisions pas ici, la librairie gamm4 peut également être utilisé pour estimer des modèles GAMMs dans R.

11.1 L’autocorrelation des résidus

L’autocorrélation des résidus désigne le degré de corrélation entre les résidus (les différences entre les valeurs réelles et les valeurs prédites) d’un modèle de série temporelle.

En d’autres termes, s’il y a autocorrélation des résidus dans un modèle de série temporelle, cela signifie qu’il existe un modèle ou une relation entre les résidus à un moment donné et les résidus à d’autres moments.

L’autocorrélation des résidus est généralement mesurée à l’aide des graphiques ACF (fonction d’autocorrélation) et pACF (fonction d’autocorrélation partielle), qui montrent la corrélation entre les résidus à différents retards.

11.1.0.1 La fonction d’autocorrélation

La fonction d’autocorrélation (ACF) d’une série temporelle stationnaire peut être définie à l’aide de l’équation suivante :

\[ACF(k) = Corr(Y_t, Y_{t-k})\] où \(Y_t\) est la valeur de la série temporelle au temps \(t\), \(Y_{t-k}\) est la valeur de la série temporelle au temps \(t-k\), et \(Corr()\) est le coefficient de corrélation entre deux variables aléatoires.

En d’autres termes, l’ACF(\(k\)) est la corrélation entre les valeurs de la série temporelle \(Y_t\) et \(Y_{t-k}\), où \(k\) est le décalage entre les deux points dans le temps. L’ACF est une mesure de l’intensité de la corrélation entre chaque valeur de la série temporelle et ses valeurs décalées à différents moments.

11.1.0.2 La fonction d’autocorrélation partielle

La fonction d’autocorrélation partielle (pACF) d’une série temporelle stationnaire peut être définie à l’aide de la formule récursive suivante :

\[pACF(1) = Corr(Y_1, Y_2)\]

\[pACF(k) = [ Corr(Y_k, Y_{k+1} - \hat{\phi}{k,1}Y{k}) ] / [ Corr(Y_1, Y_2 - \hat{\phi}_{1,1}Y_1) ]\]

pour \(k > 1\)

où \(Y_t\) est la valeur de la série temporelle au temps \(t\), \(\hat{\phi}{k,1}\), \(\hat{\phi}{1,1}\), \(...\) \(\hat{\phi}{k-1,k-1}\) sont les coefficients du modèle autorégressif d’ordre \(k-1\) ajusté à la série temporelle, et \(Corr()\) est le coefficient de corrélation entre deux variables aléatoires.

En d’autres termes, le pACF(\(k\)) est la corrélation entre les valeurs des séries temporelles \(Y_k\) et \(Y_{k+j}\) après suppression de l’influence des décalages intermédiaires \(Y_{k+1}, Y_{k+2}, ..., Y_{k+j-1}\) à l’aide d’un modèle autorégressif d’ordre \(k-1\). Le pACF mesure la corrélation entre \(Y_k\) et \(Y_{k+j}\) après avoir éliminé l’effet de tout délai intermédiaire plus court.

Si les graphiques ACF ou pACF montrent des corrélations significatives à des retards non nuls, il y a des preuves d’autocorrélation des résidus et le modèle peut devoir être modifié ou amélioré pour mieux capturer les modèles sous-jacents dans les données.

Voyons comment cela fonctionne avec notre modèle year_gam!

Pour commencer, nous allons jeter un coup d’œil à un modèle avec de l’autocorrélation temporelle dans les résidus. Revenons au modèle de la température de Nottingham pour vérifier si les résidus sont corrélés en faisant appel à la fonction (partielle) d’autocorrélation.

par(mfrow = c(1, 2))
acf(resid(year_gam), lag.max = 36, main = "ACF")
pacf(resid(year_gam), lag.max = 36, main = "pACF")

Dans le graphique ACF, la région ombrée en bleu représente l’intervalle de confiance et les lignes rouges en pointillé représentent les limites de la signification statistique.

La fonction d’autocorrelaton (ACF; première figure) évalue la corrélation croisée d’une série temporelle entre points à différents décalages (donc, la similarité entre observations progressivement décalés).

En contraste, la fonction partielle d’autocorrelation (PACF: deuxième figure) évalue la corrélation croisée d’une série temporelle entre points à différents décalages, après avoir contrôlé les valeurs de la série temporelle à tous les décalages plus courts.

Les graphiques ACF et pACF sont donc utilisés pour identifier le temps nécessaire avant que les observations ne sont plus autocorrélées.

Les graphiques des fonctions d’autocorrélation suggèrent qu’un modèle AR de faible ordre est nécessaire (avec un ou deux intervalles de temps décalés).

Nous pouvons tester cet hypothèse en ajoutant des structures d’autocorrelation au modèle de température de Nottingham. Créons un modèle AR(1) (corrélation à 1 intervalle de temps décalé), et un modèle AR(2) (corrélation à 2 intervalles de temps décalés), et comparons-les avec AIC pour déterminer le modèle le mieux ajusté.

df <- data.frame(nottem, nottem_year, nottem_month)

year_gam <- gamm(nottem ~ s(nottem_year) + s(nottem_month, bs = "cc"),
    data = df)

year_gam_AR1 <- gamm(nottem ~ s(nottem_year) + s(nottem_month,
    bs = "cc"), correlation = corARMA(form = ~1 | nottem_year,
    p = 1), data = df)

year_gam_AR2 <- gamm(nottem ~ s(nottem_year) + s(nottem_month,
    bs = "cc"), correlation = corARMA(form = ~1 | nottem_year,
    p = 2), data = df)

Quel modèle est mieux ajusté?

AIC(year_gam$lme, year_gam_AR1$lme, year_gam_AR2$lme)

##                  df      AIC
## year_gam$lme      5 1109.908
## year_gam_AR1$lme  6 1101.218
## year_gam_AR2$lme  7 1101.598

Le modèle avec la structure AR(1) donne un meilleur ajustement comparé au premier modèle (year_gam), il y a très peu d’amélioration en passant au AR(2). Il est donc préférable d’inclure uniquement la structure AR(1) dans notre modèle.

11.2 Modélisation avec effets mixtes

Comme nous l’avons vu dans la section précédente, bs spécifie la fonction de base sous-jacente. Pour les facteurs aléatoires (origine et pente linéaire), nous utilisons bs = "re" et pour les pentes aléatoires non linéaires, nous utilisons bs = "fs".

Trois types d’effets aléatoires différents sont possibles lors de l’utilisation des GAMMs (où fac représente une variable qualitative utilisée pou l’effet aléatoire et x0 est un effet quantitatif fixe) :

interceptes aléatoires ajustent la hauteur des termes du modèle avec une valeur constante de pente : s(fac, bs = "re")
pentes aléatoires ajustent la pente d’une variable explicative numérique: s(fac, x0, bs = "re")
surfaces lisses aléatoires ajustent la tendance d’une prédiction numérique de façon non linéaire: s(x0, fac, bs = "fs", m = 1) où l’argument \(m=1\) met une plus grande pénalité au lissage qui s’éloigne de 0, ce qui entraîne un retrait vers la moyenne.

Pour plus de détails sur les effets aléatoires, voir l’Atelier 7.

Ceci est une introduction (très!) brève aux effets aléatoires dans les GAMMs. Pour plus de détails, nous recommandons fortement Pedersen et al. (2019), un article très accessible qui décrit plusieurs façons de spécifier des GAMMs pour répondre à des questions écologiques.

11.2.1 GAMM avec un intercepte aléatoire

Nous allons utiliser gamSim() pour générer un ensemble de données, cette fois-ci avec un effet aléatoire. Ensuite, nous construirons un modèle avec un intercepte aléatoire en utilisant fac comme facteur aléatoire.

# Simuler des données
gam_data2 <- gamSim(eg = 6)

## 4 term additive + random effectGu & Wahba 4 term additive model

head(gam_data2)

##           y        x0        x1         x2        x3        f        f0
## 1  7.518584 0.8207924 0.2449618 0.07052723 0.3464905  7.38789 1.0674464
## 2  8.729694 0.9689549 0.2218811 0.70986072 0.6179543 10.51996 0.1947529
## 3 19.970161 0.2852750 0.5747120 0.45505182 0.8551117 16.80216 1.5619408
## 4 15.103731 0.4287817 0.3003228 0.60491872 0.9581833 18.99721 1.9501494
## 5  9.793633 0.2313136 0.8460123 0.79673569 0.2244902 10.91826 1.3288034
## 6 22.660200 0.6597815 0.8035586 0.35742106 0.5001123 18.39322 1.7532743
##         f1       f2 f3 fac
## 1 1.632192 1.688252  0   1
## 2 1.558560 2.766648  0   2
## 3 3.156374 3.083846  0   3
## 4 1.823296 3.223768  0   4
## 5 5.430464 1.158996  0   1
## 6 4.988410 5.651538  0   2

# Rouler un modèle avec intercepte aléatoire
gamm_intercept <- gam(y ~ s(x0) + s(fac, bs = "re"), data = gam_data2,
    method = "REML")

# Voir la sortie du modèle
summary(gamm_intercept)$s.table

##             edf  Ref.df         F    p-value
## s(x0)  2.458656 3.06275  2.628241 0.04953447
## s(fac) 2.964557 3.00000 83.678846 0.00000000

Notez qu’il y a maintenant un terme aléatoire dans le sommaire du modèle. Vous pouvez visualiser les intercepts aléatoires pour chaque niveau de fac comme ceci:

plot(gamm_intercept, select = 2)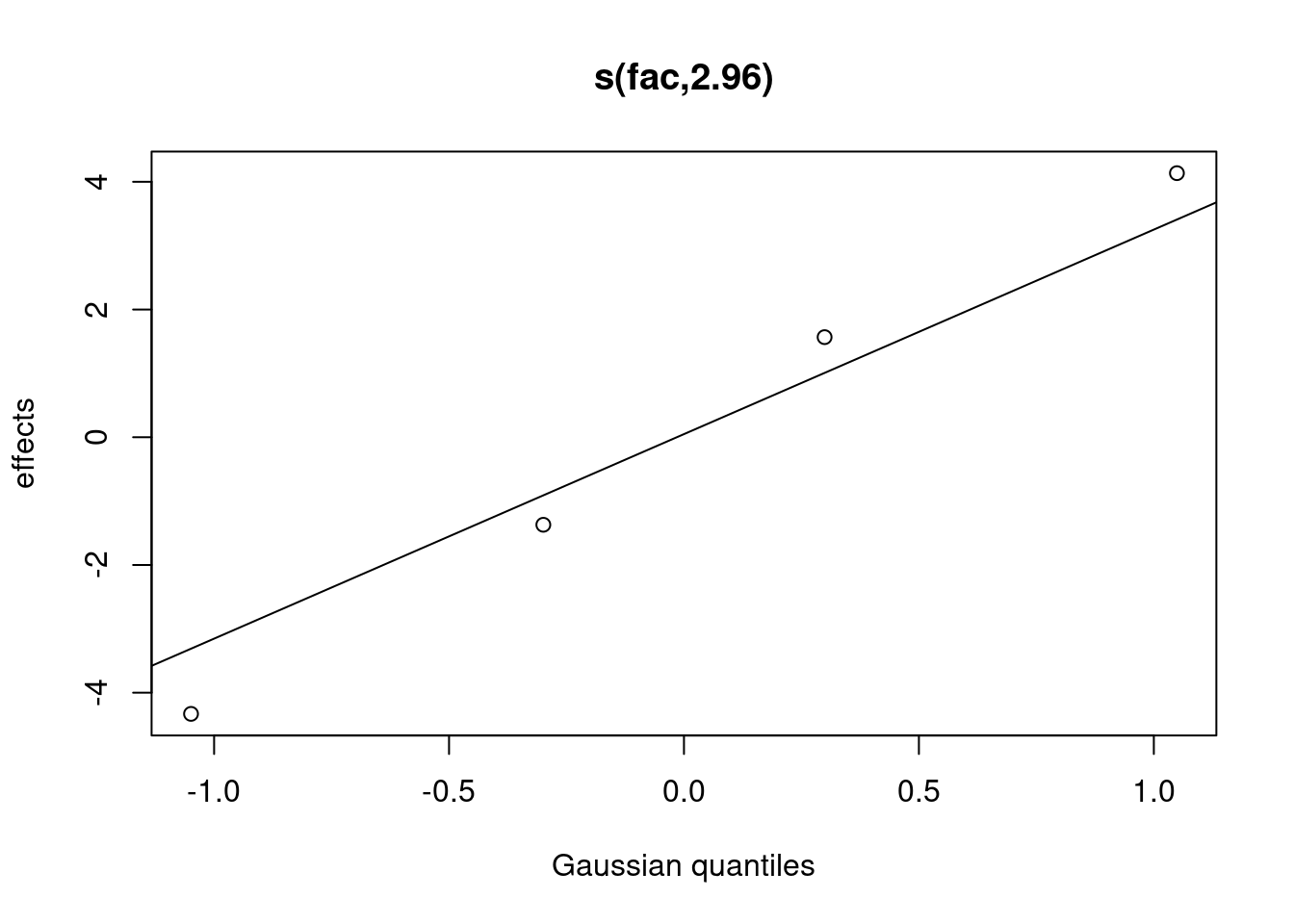

# select = 2 parce que le terme aléatoire se trouve sur la
# 2e ligne du tableau sommaire.

Nous pouvons également utiliser la fonction plot_smooth pour visualiser le modèle, qui nous permet de visualisés des effets sommés d’un GAM (basé sur les prédictions). Cette fonction permet également de supprimer les effets aléatoires en définissant rm.ranef = TRUE.

On peut premièrement visualiser l’effet combiné de x0 sans les niveaux de l’effet aléatoire, et ensuite une courbe pour chacun de quatre niveaux de l’effet aléatoire fac:

par(mfrow = c(1, 2), cex = 1.1)

# Visualiser les effets combinés de x0 (sans effets
# aléatoires)
plot_smooth(gamm_intercept, view = "x0", rm.ranef = TRUE, main = "intercept + s(x1)")

# Visualiser chaque niveau de l'effet aléatoire
plot_smooth(gamm_intercept, view = "x0", rm.ranef = FALSE, cond = list(fac = "1"),
    main = "... + s(fac)", col = "orange", ylim = c(0, 25))
plot_smooth(gamm_intercept, view = "x0", rm.ranef = FALSE, cond = list(fac = "2"),
    add = TRUE, col = "red")
plot_smooth(gamm_intercept, view = "x0", rm.ranef = FALSE, cond = list(fac = "3"),
    add = TRUE, col = "purple")
plot_smooth(gamm_intercept, view = "x0", rm.ranef = FALSE, cond = list(fac = "4"),
    add = TRUE, col = "turquoise")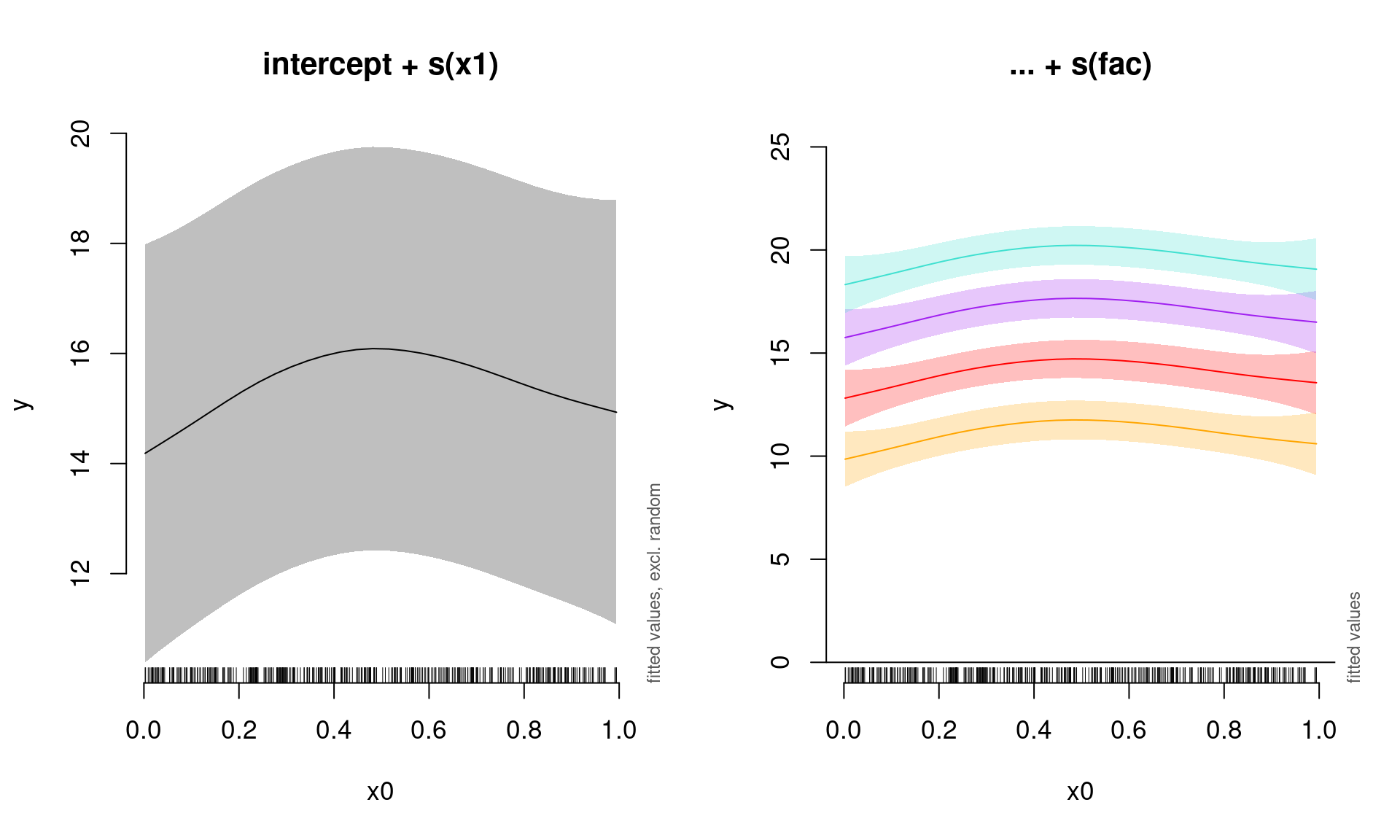

11.2.2 GAMM avec une pente aléatoire

Ensuite, spécifions un modèle avec une pente aléatoire:

gamm_slope <- gam(y ~ s(x0) + s(x0, fac, bs = "re"), data = gam_data2,
    method = "REML")

summary(gamm_slope)$s.table

##                edf   Ref.df         F    p-value
## s(x0)     2.580092 3.213344  2.767091 0.03955472
## s(x0,fac) 2.934112 3.000000 45.541826 0.00000000

On peut encore une fois visualiser l’effet combiné de x0 sans les niveaux de l’effet aléatoire, et ensuite une courbe pour chacun de quatre niveaux de l’effet aléatoire fac:

par(mfrow = c(1, 2), cex = 1.1)

# Visualiser les effets combinés de x0 (sans effets
# aléatoires)
plot_smooth(gamm_slope, view = "x0", rm.ranef = TRUE, main = "intercept + s(x1)")

# Visualiser chaque niveau de l'effet aléatoire
plot_smooth(gamm_slope, view = "x0", rm.ranef = FALSE, cond = list(fac = "1"),
    main = "... + s(fac, x0)", col = "orange", ylim = c(0, 25))
plot_smooth(gamm_slope, view = "x0", rm.ranef = FALSE, cond = list(fac = "2"),
    add = TRUE, col = "red")
plot_smooth(gamm_slope, view = "x0", rm.ranef = FALSE, cond = list(fac = "3"),
    add = TRUE, col = "purple")
plot_smooth(gamm_slope, view = "x0", rm.ranef = FALSE, cond = list(fac = "4"),
    add = TRUE, col = "turquoise")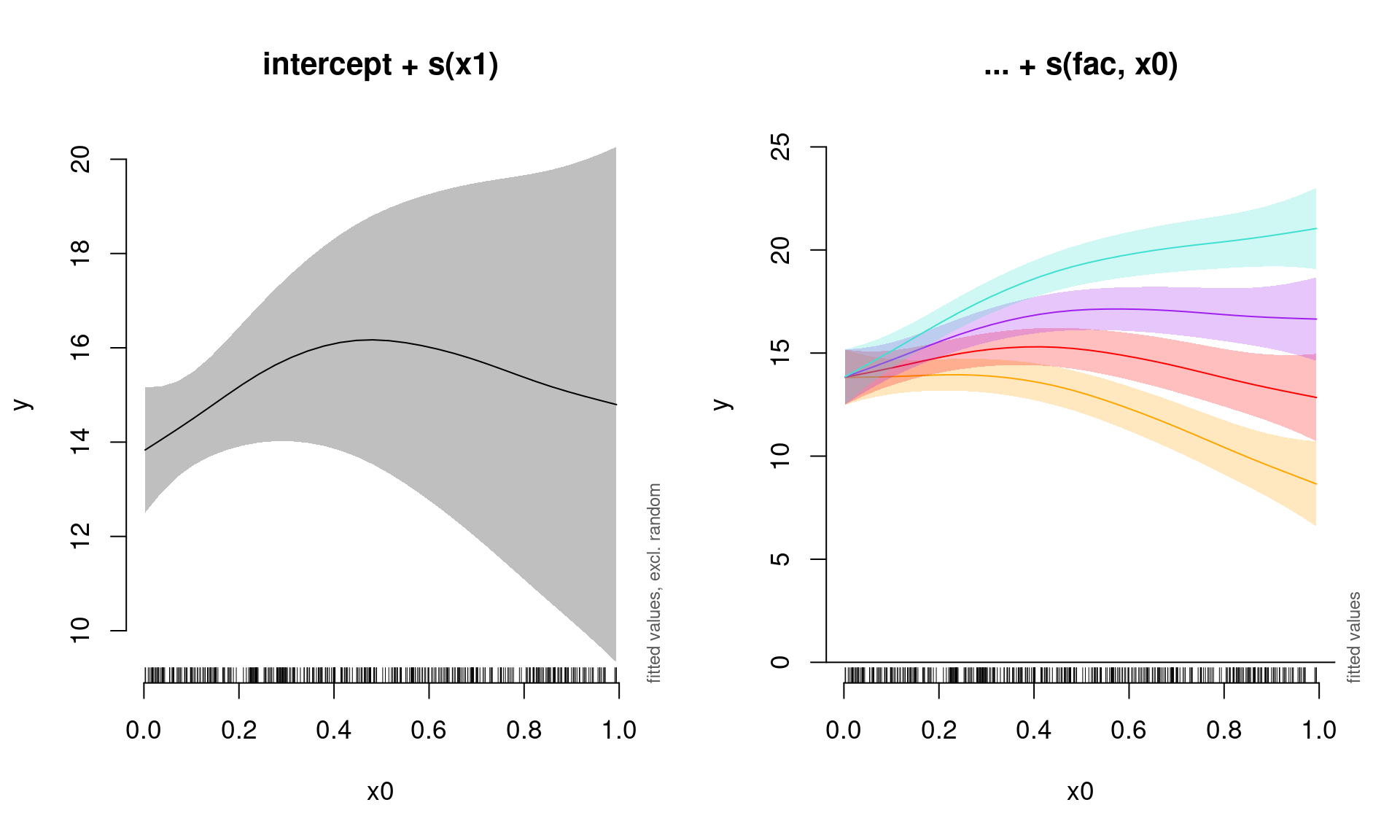

11.2.3 GAMM avec un intercept et une pente aléatoire

On peut aussi inclure un intercept et une pente aléatoire.

gamm_int_slope <- gam(y ~ s(x0) + s(fac, bs = "re") + s(fac,
    x0, bs = "re"), data = gam_data2, method = "REML")

summary(gamm_int_slope)$s.table

##                  edf  Ref.df          F    p-value
## s(x0)     2.45837570 3.06234  2.6207107 0.05004079
## s(fac)    2.96218841 3.00000 90.6373364 0.00000000
## s(fac,x0) 0.08373958 3.00000  0.1963193 0.32113844

On peut encore une fois visualiser l’effet combiné de x0 sans les niveaux de l’effet aléatoire, et ensuite une courbe pour chacun de quatre niveaux de l’effet aléatoire fac:

par(mfrow = c(1, 2), cex = 1.1)

# Visualiser les effets combinés de x0 (sans effets
# aléatoires)
plot_smooth(gamm_int_slope, view = "x0", rm.ranef = TRUE, main = "intercept + s(x1)")

# Visualiser chaque niveau de l'effet aléatoire
plot_smooth(gamm_int_slope, view = "x0", rm.ranef = FALSE, cond = list(fac = "1"),
    main = "... + s(fac) + s(fac, x0)", col = "orange", ylim = c(0,
        25))
plot_smooth(gamm_int_slope, view = "x0", rm.ranef = FALSE, cond = list(fac = "2"),
    add = TRUE, col = "red")
plot_smooth(gamm_int_slope, view = "x0", rm.ranef = FALSE, cond = list(fac = "3"),
    add = TRUE, col = "purple")
plot_smooth(gamm_int_slope, view = "x0", rm.ranef = FALSE, cond = list(fac = "4"),
    add = TRUE, col = "turquoise")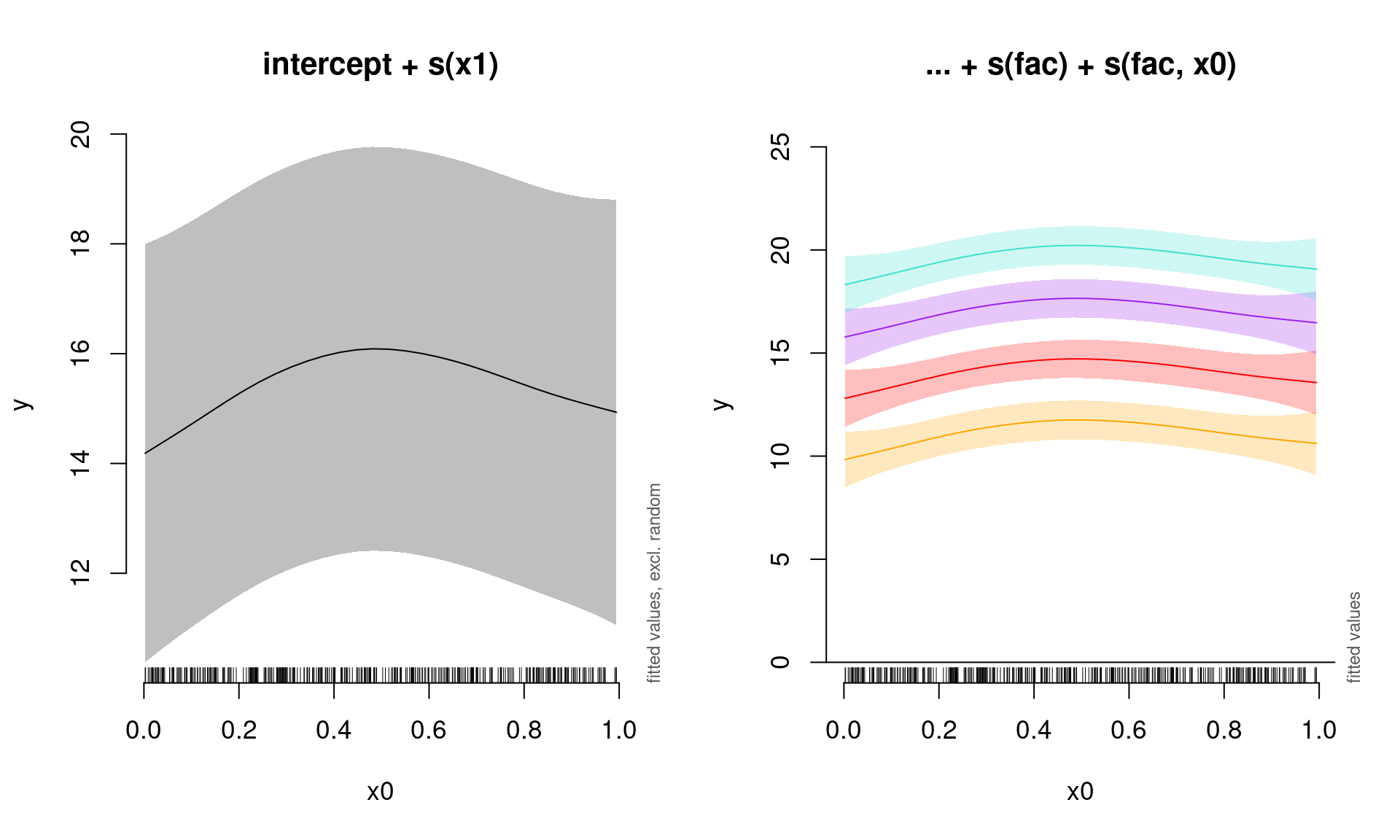

Notez que la pente aléatoire est statique dans ce cas:

plot(gamm_int_slope, select = 3)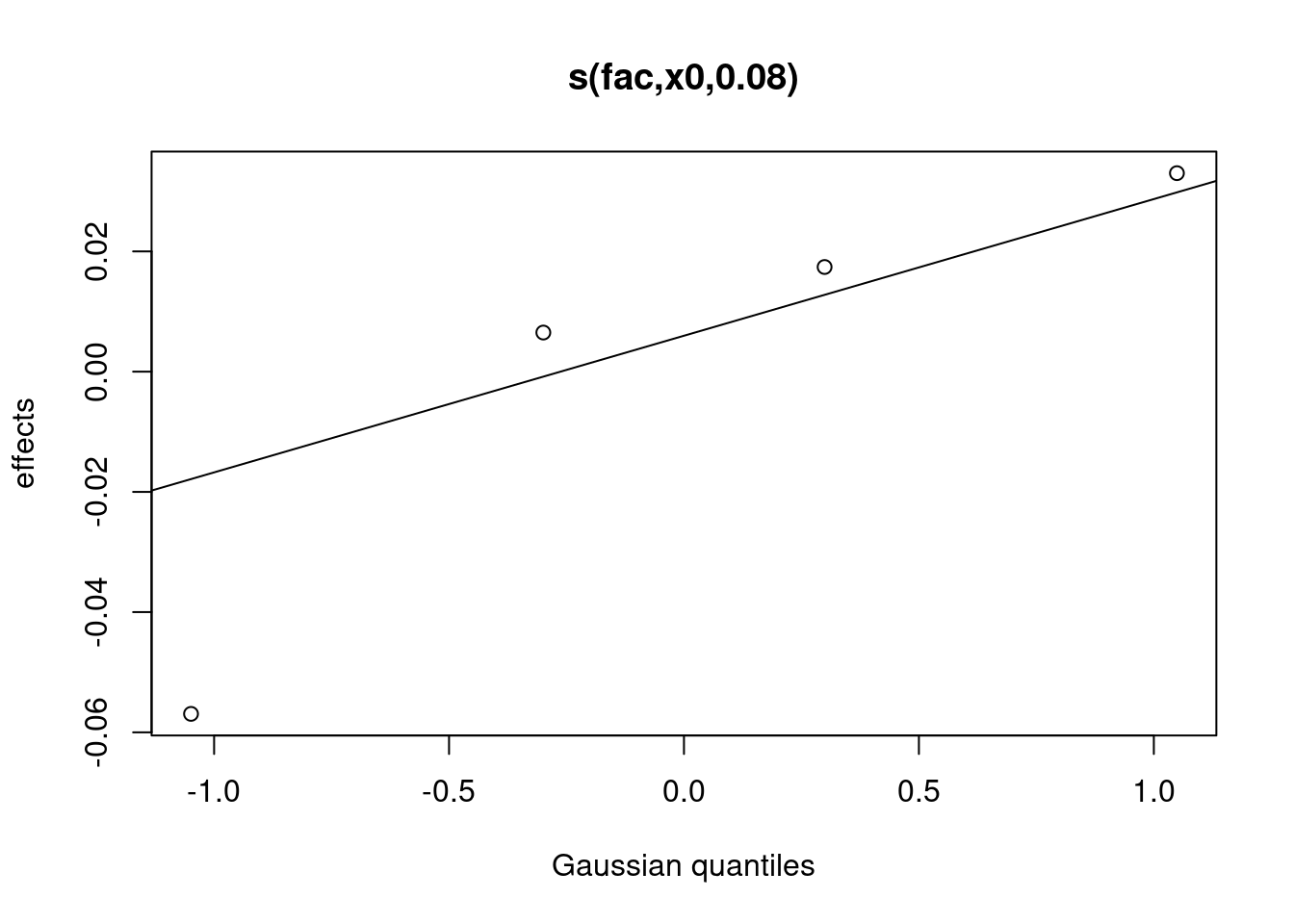

# select = 3 parce que la pente aléatoire est sur la
# troisième ligne de notre tableau sommaire.

11.2.4 GAMM avec une surface lisse aléatoire

Finalement, spécifions un modèle avec une surface lisse aléatoire.

gamm_smooth <- gam(y ~ s(x0) + s(x0, fac, bs = "fs", m = 1),
    data = gam_data2, method = "REML")

## Warning in gam.side(sm, X, tol = .Machine$double.eps^0.5): model has repeated
## 1-d smooths of same variable.

summary(gamm_smooth)$s.table

##                edf    Ref.df        F  p-value
## s(x0)     2.132647  2.534099 1.518021 0.256472
## s(x0,fac) 9.940991 35.000000 7.786533 0.000000

Si la pente aléatoire variait selon x0, on verrait différentes courbes pour chaque niveau:

plot(gamm_smooth, select = 1)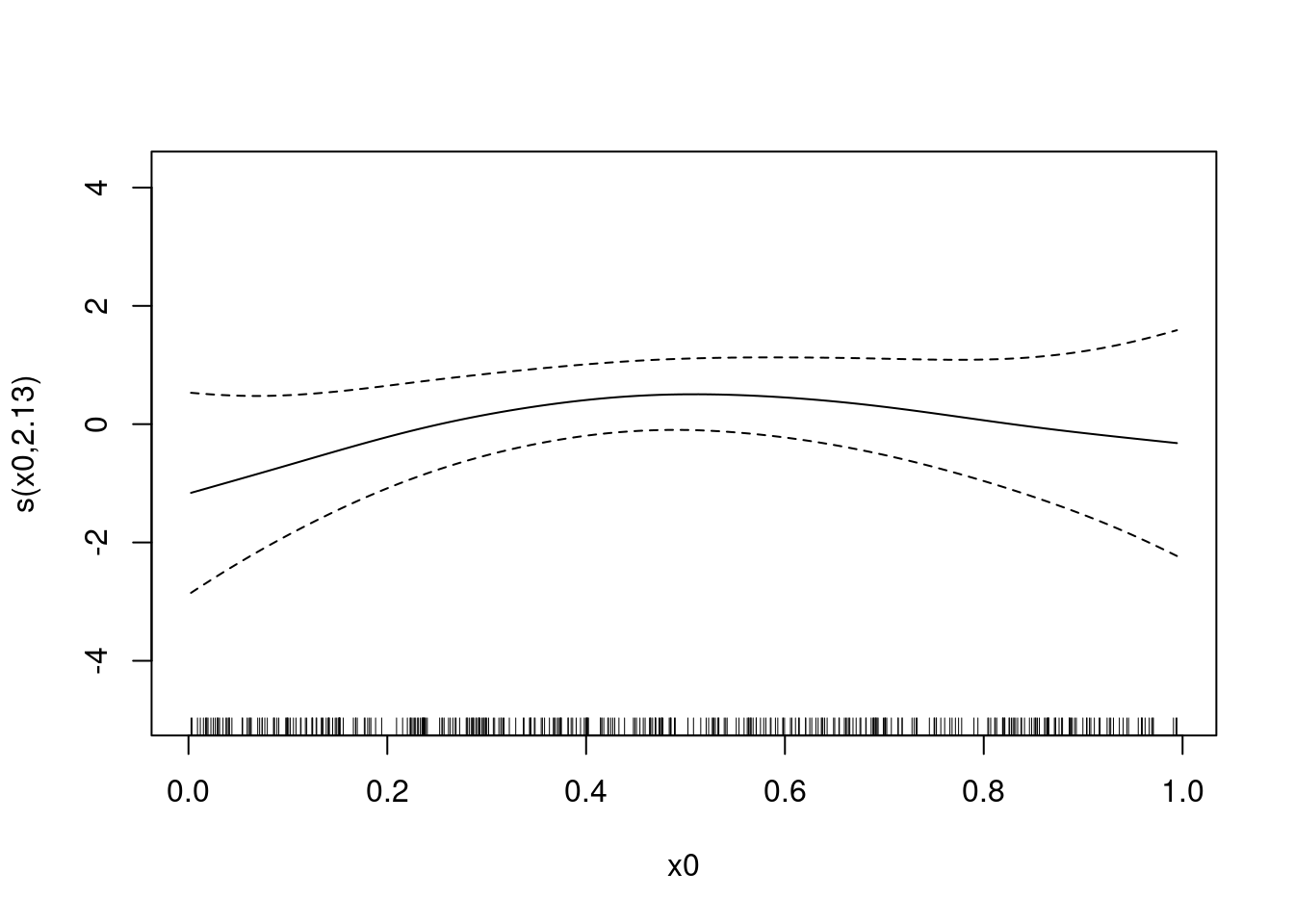

# select = 1 parce que la surface lisse aléatoire est sur
# la première ligne de notre tableau sommaire.

On peut encore une fois visualiser l’effet combiné de x0 sans les niveaux de l’effet aléatoire, et ensuite une courbe pour chacun de quatre niveaux de l’effet aléatoire fac:

par(mfrow = c(1, 2), cex = 1.1)

# Visualiser les effets combinés de x0 (sans effets
# aléatoires)
plot_smooth(gamm_smooth, view = "x0", rm.ranef = TRUE, main = "intercept + s(x1)")

# Visualiser chaque niveau de l'effet aléatoire
plot_smooth(gamm_smooth, view = "x0", rm.ranef = FALSE, cond = list(fac = "1"),
    main = "... + s(fac) + s(fac, x0)", col = "orange", ylim = c(0,
        25))
plot_smooth(gamm_smooth, view = "x0", rm.ranef = FALSE, cond = list(fac = "2"),
    add = TRUE, col = "red")
plot_smooth(gamm_smooth, view = "x0", rm.ranef = FALSE, cond = list(fac = "3"),
    add = TRUE, col = "purple")
plot_smooth(gamm_smooth, view = "x0", rm.ranef = FALSE, cond = list(fac = "4"),
    add = TRUE, col = "turquoise")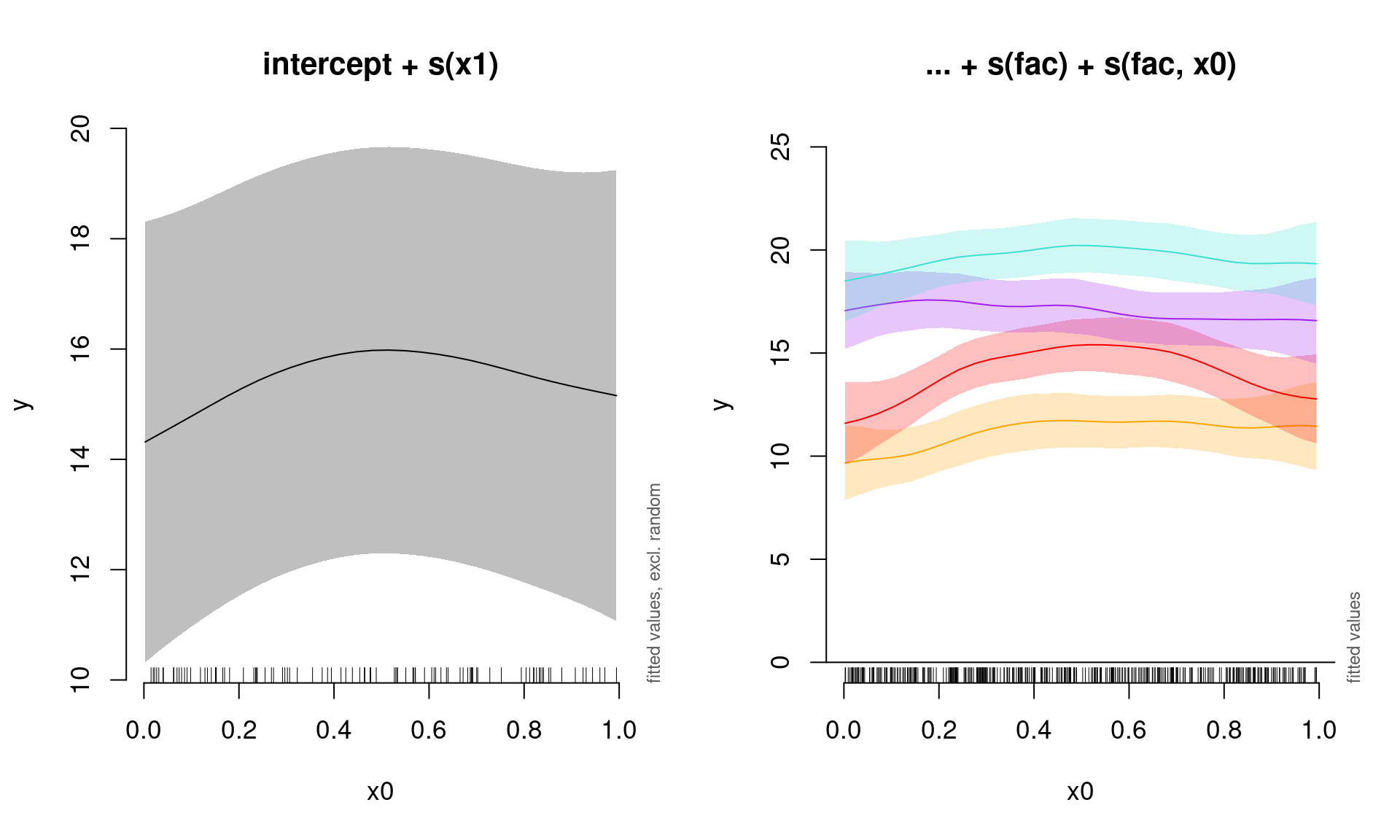

11.2.5 Comparaison de GAMM

Tous les GAMMs de cette section peuvent être comparé avec AIC() pour trouver le modèle le mieux ajusté:

AIC(gamm_intercept, gamm_slope, gamm_int_slope, gamm_smooth)

##                       df      AIC
## gamm_intercept  7.990398 2257.388
## gamm_slope      8.080896 2334.800
## gamm_int_slope  8.221835 2257.663
## gamm_smooth    16.643505 2255.081

Le meilleur modèle de ces trois modèles serait donc le GAMM avec un intercept aléatoire.

References

Pedersen, Eric J, David L Miller, Gavin L Simpson, and Noam Ross. 2019. “Hierarchical Generalized Additive Models in Ecology: An Introduction with Mgcv.” PeerJ 7: e6876.