Chapitre 7 GAM avec des termes d’interaction

Il y a deux façons de modéliser une interaction entre deux variables :

pour deux variables non-linéaire : s(x1, x2)
pour une variable non-linéaire et une variable linéaire (quantitative ou qualitative) : utiliser l’argument by, s(x1, by = x2)
- Quand x2 est qualitative, vous avez un terme non linéaire qui varie entre les différents niveaux de x2
- Quand x2 est quantitative, l’effet linéaire de x2 varie avec x1
- Quand x2 est qualitative, le facteur doit être ajouté comme effet principal dans le modèle

7.1 Interaction entre variables non-linéaire et qualitatif

Nous allons examiner l’effet de l’interaction en utilisant notre variable qualitative Season et examiner si la non-linéarité de s(SampleDepth) varie selon les différents niveaux de Season.

factor_interact <- gam(Sources ~ Season + s(SampleDepth, by = Season) +
    s(RelativeDepth), data = isit, method = "REML")

summary(factor_interact)$s.table

##                             edf   Ref.df          F p-value
## s(SampleDepth):Season1 6.839386 7.552045  95.119422       0
## s(SampleDepth):Season2 8.744574 8.966290 154.474325       0
## s(RelativeDepth)       6.987223 8.055898   6.821074       0

par(mfrow = c(2, 2))
plot(factor_interact)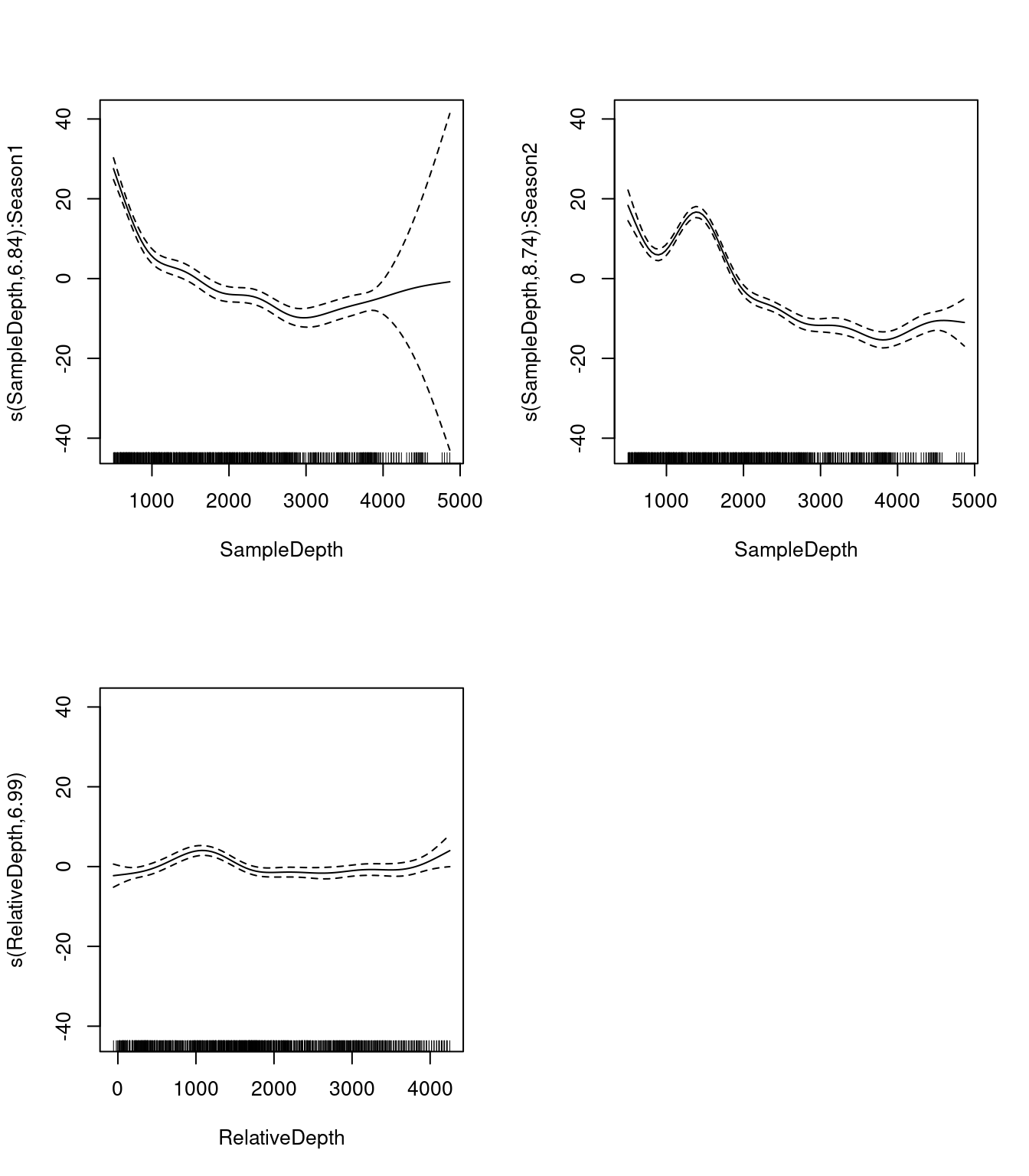

Les deux premiers graphiques montrent l’effet d’interaction entre notre variable lisse SampleDepth et chaque niveau de notre variable factorielle, Season. Voyez-vous une différence entre les deux courbes ?

Les graphiques montrent quelques différences entre la forme des termes lisses entre les deux niveaux de Season. La différence la plus notable est le pic dans le deuxième panneau, qui nous indique qu’il y a un effet de SampleDepth entre 1000 et 2000 qui est important dans la saison 2, mais qui ne se produit pas dans la saison 1. Ceci suggère que l’effet d’interaction pourrait être important à inclure dans notre modèle.

Nous pouvons également représenter l’effet d’interaction en 3D sur un seul graphique, en utilisant vis.gam().

vis.gam(factor_interact, theta = 120, n.grid = 50, lwd = 0.4)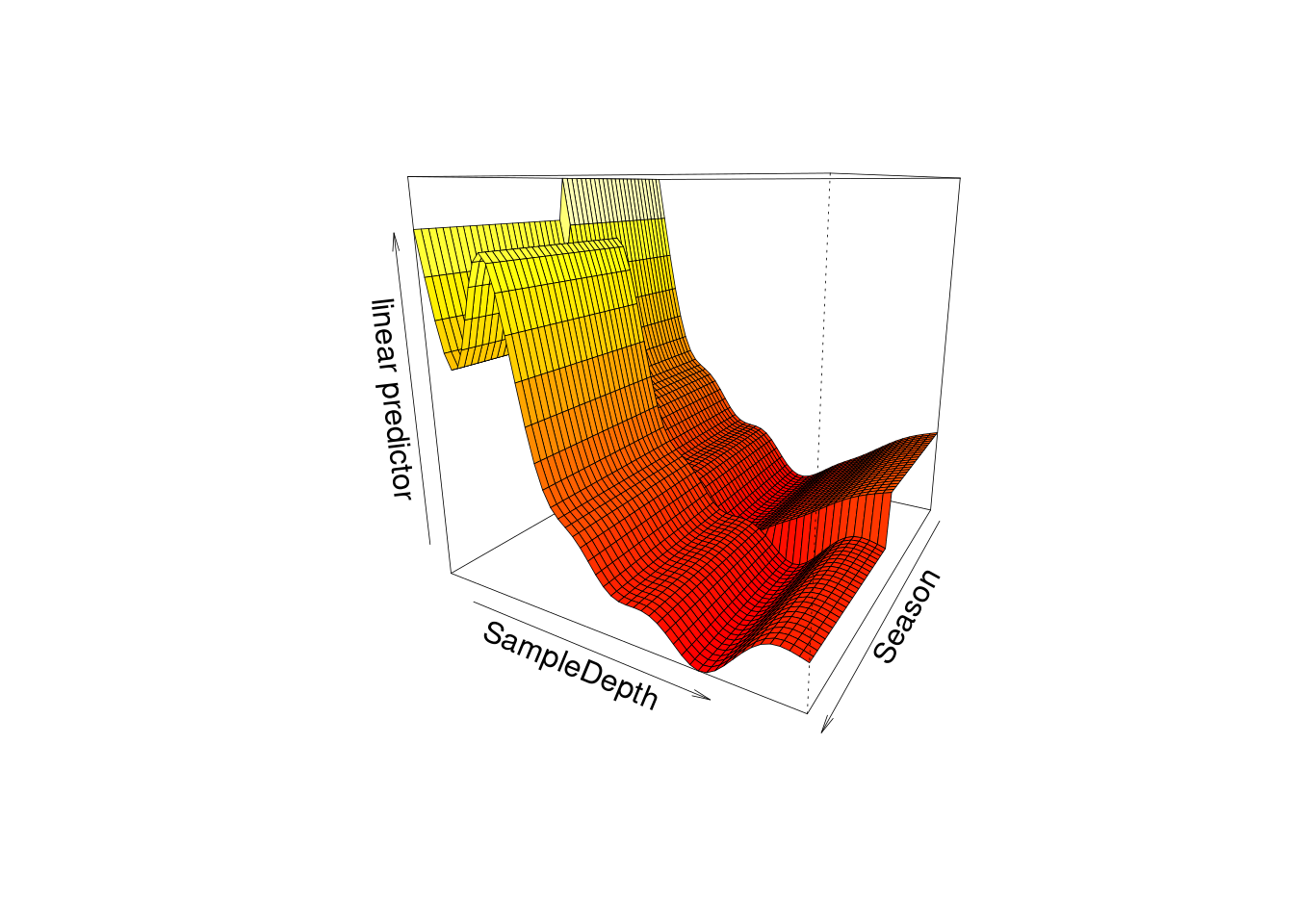

On peut changer le degré de rotation de notre plan x-y avec l’argument theta.

Pour vérifier notre hypothèse que cette interaction est importante, on peut faire une comparaison de modèles en utilisant l’AIC pour déterminer si le terme d’interaction améliore la performance de notre modèle.

AIC(two_smooth_model, factor_interact)

##                        df      AIC
## two_smooth_model 20.46960 5056.841
## factor_interact  26.99693 4878.631

L’AIC de notre modèle avec une interaction factorielle entre le lisse SampleDepth et le Season a un score AIC plus bas, ce qui nous indique que ce modèle est plus performant que two_smooth_model. L’inclusion de cette interaction améliore la performance de notre modèle.

7.2 Interaction entre variables non linéaires

Finalement, nous regardons les interactions entre deux termes non linéaires, SampleDepth et RelativeDepth.

smooth_interact <- gam(Sources ~ Season + s(SampleDepth, RelativeDepth),
    data = isit, method = "REML")
summary(smooth_interact)$s.table

##                                   edf Ref.df        F p-value
## s(SampleDepth,RelativeDepth) 27.12521  28.77 93.91722       0

Dans la section précédente, nous avons pu visualiser un effet d’interaction entre un terme non linéaire et un terme factoriel en dessinant une fonction lisse différente de SampleDepth pour chaque niveau de Season.

Dans ce modèle, nous avons deux termes non linéaires, donc l’effet de SampleDepth varie de façon linéaire avec RelativeDepth, et vice-versa. Lorsque nous visualisons cette interaction, nous obtenons plutôt un gradient entre deux fonctions continues lissées :

plot(smooth_interact, page = 1, scheme = 2)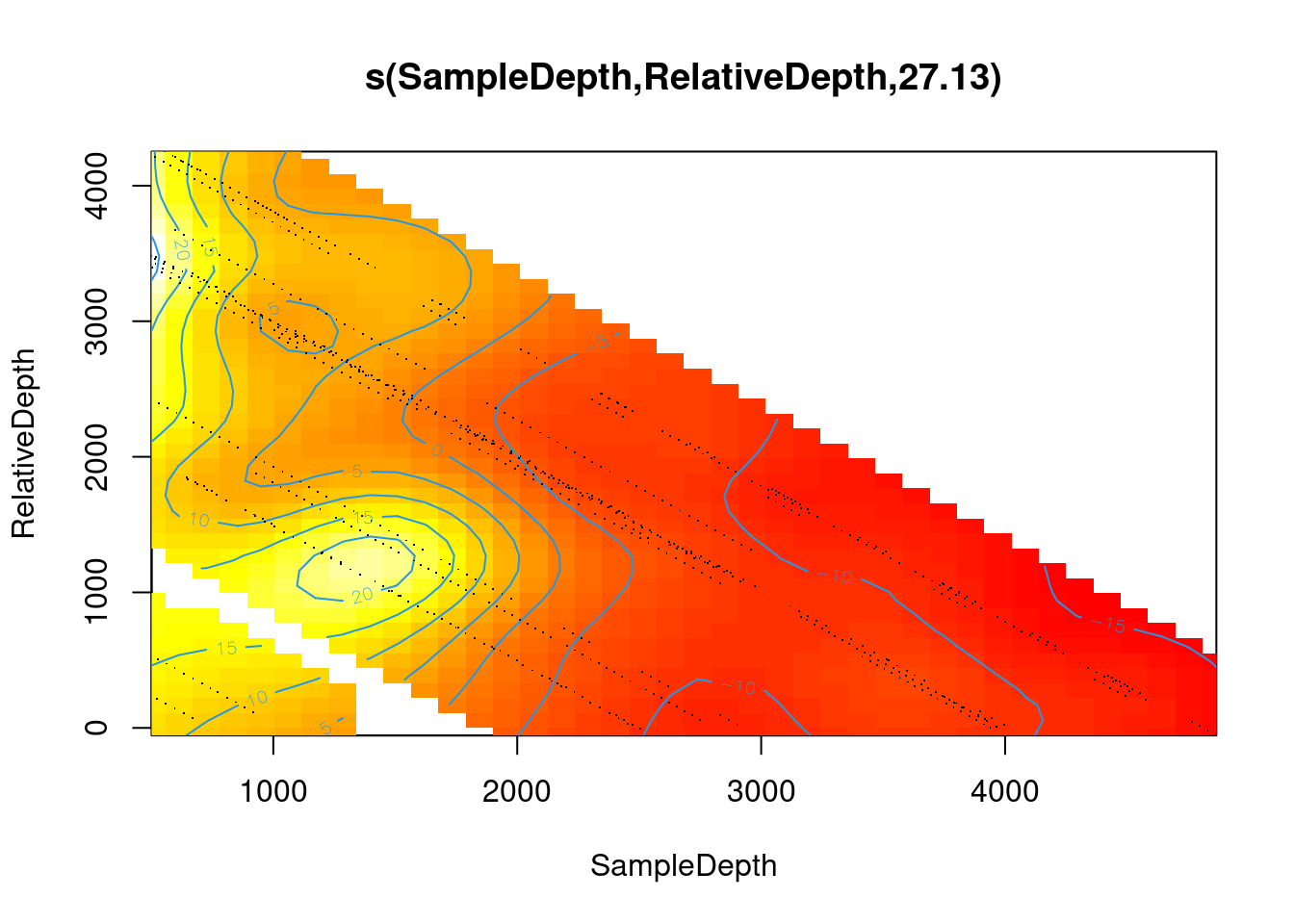

We can also plot this interaction on a 3D surface:

vis.gam(smooth_interact, view = c("SampleDepth", "RelativeDepth"),
    theta = 50, n.grid = 50, lwd = 0.4)

Rappelez-vous, ce graphique peut être réorienté en changeant la valeur de l’argument theta.

On peut changer la couleur du graphique 3D en utilisant l’argument color. Essayez de spécifier color = "cm" dans vis.gam() ci-dessus, et consultez ?vis.gam pour plus d’options de couleurs.

Les graphiques illustrent une interaction non linéaire, où Sources est plus faible à des valeurs élevées de SampleDepth et RelativeDepth, mais augmente avec RelativeDepth alors que SampleDepth est faible.

Ainsi, il semble y avoir un effet d’interaction entre ces termes non linéaires. Est-ce que l’inclusion de l’interaction entre s(SampleDepth) et s(RelativeDepth) améliore notre modèle two_smooth_model?

AIC(two_smooth_model, smooth_interact)

##                        df      AIC
## two_smooth_model 20.46960 5056.841
## smooth_interact  30.33625 4943.890

Le modèle avec l’interaction entre s(SampleDepth) et s(RelativeDepth) a un AIC inférieur, ce qui signifie que l’inclusion de cette interaction améliore la performance de notre modèle, et notre capacité à comprendre les déterminants de la bioluminescence.