Chapitre 3 Le modèle linéaire… et où il échoue

Que veut-on dire par “modèle linéaire”? La régression est la base des statistiques. La régression linéaire est ce que la plupart des gens apprennent avant tout en statistiques et est parmi les méthodes les plus performantes. Elle nous permet de modéliser une variable réponse en fonction de facteurs prédictifs et d’une erreur résiduelle.

Comme on a vu dans l’Atelier 4: Modèles linéaires, le modèle linéaire fait quatre suppositions importantes:

Relation linéaire entre les variables de réponse et les variables prédicteurs: \[y_i = \beta_0 + \beta_1 \times x_i + \epsilon_i\]
L’erreur est distribuée normalement: \[\epsilon_i \sim \mathcal{N}(0,\,\sigma^2)\]
La variance des erreurs est constante
Chaque erreur est indépendante des autres (homoscédasticité)

Un modèle linéaire peut parfois s’adapter à certains types de réponses non linéaires (par exemple \(x^2\)), mais cette approche repose fortement sur des décisions qui peuvent être soit arbitraires, soit bien informées, et est beaucoup moins flexible que l’utilisation d’un modèle additif. Par exemple, ce modèle linéaire à prédicteurs multiples peut traiter une réponse non linéaire, mais devient rapidement difficile à interpréter et à maîtriser:

\[y_i = \beta_0 + \beta_1x_{1,i}+\beta_2x_{2,i}+\beta_3x_{3,i}+...+\beta_kx_{k,i} + \epsilon_i\]

Les modèles linéaires fonctionnent très bien dans certains cas spécifiques où tous ces critères sont respectés:

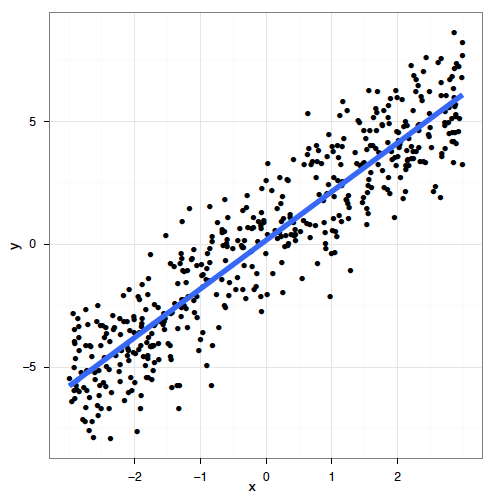
En réalité, il est souvent impossible de respecter ces critères. Dans de nombreux cas, les modèles linéaires sont inappropriés:

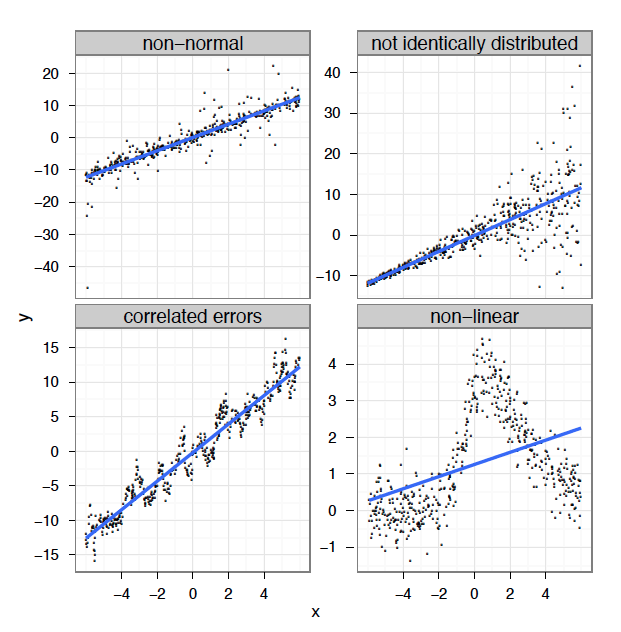
Alors, comment résoudre ce problème ? Pour répondre à cette question, nous devons d’abord considérer ce que le modèle de régression tente de faire. Un modèle linéaire essaye d’ajuster la meilleure droite qui passe au milieu des données sans sur-ajuster les données, ce qui se produirait si nous tracions simplement une ligne entre chaque point et ses voisins.

En revanche, les modèles additifs (GAM) ajustent une fonction de lissage non-linéaire à travers les données, tout en contrôlant le degré de courbure de la ligne our éviter un ajustement excessif. Les modèles additifs peuvent donc capturer des relations non linéaires en ajustant une fonction lisse à travers les données, plutôt qu’une ligne droite. Nous reviendrons plus tard sur le degré de courbure de la ligne!