Chapitre 6 Les distributions des données biologiques

Les statisticiens ont développé une foule de lois de probabilité (ou distributions) correspondant à divers types de données. Une loi de probabilité donne la probabilité d’observer chaque issue possible d’une expérience ou campagne d’échantillonage (par. ex. abondance = 8 Galumna est un issu d’un échantillonage). Les lois «discrètes» n’incluent que des nombres entiers dans leur ensemble d’issus, alors que les lois «continues» incluent aussi des fractions (par. ex. la loi normale). Toutes les lois ont des paramètres qui déterminent la forme de la loi/distribution (par. ex. μ et σ2 pour la loi normale). Pour un excellent survol des lois de probabilités utiles en écologie, nous vous recommandons le chapitre 4 du livre de Ben Bolker Ecological Models and Data in R. Ici nous ne présenterons que brièvement quelques distributons utiles pour les GLMs.

Nous avons déjà vu que notre variable «abondance de Galumna» ne peut prendre comme valeur que des nombres entiers, et serait donc mieux modélisée par une loi discrète qu’une loi continue. Une loi utile pour modéliser les données d’abondance est la loi de «Poisson», nommé en l’honneur du statisticien Siméon Denis Poisson. La loi de Poisson est une loi discrète avec un seul paramètre: $\lambda$ (lambda), qui détermine et la moyenne et la variance de la distribution (la moyenne et la variance d’une loi de Poisson sont donc égales). Voici 3 exemples de lois de Poisson avec des valeurs différentes de $\lambda$, ce qui correspond ici au nombre moyen de Galumna retrouvé dans un ensemble fictif d’échantillons:

# examples of Poisson distributions with different values
# of lambda
par(cex = 2)
x = seq(1, 50, 1)
plot(x, dpois(x, lambda = 1), type = "h", lwd = 3, xlab = "Frequency of Galumna",
    ylab = "Probability", main = "lambda = 1")
plot(x, dpois(x, lambda = 10), type = "h", lwd = 3, xlab = "Frequency of Galumna",
    ylab = "Probability", main = "lambda = 10")
plot(x, dpois(x, lambda = 30), type = "h", lwd = 3, xlab = "Frequency of Galumna",
    ylab = "Probability", main = "lambda = 30")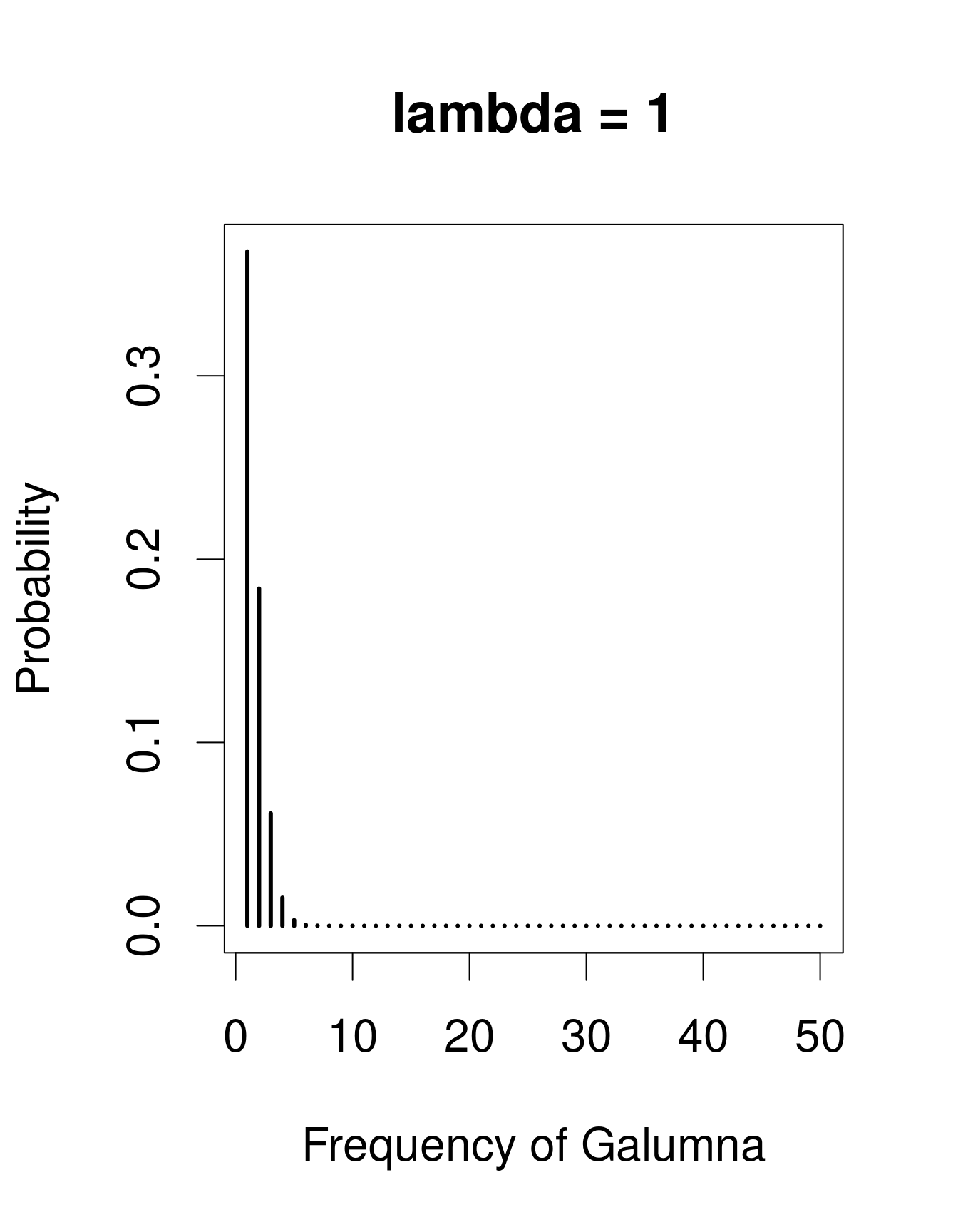

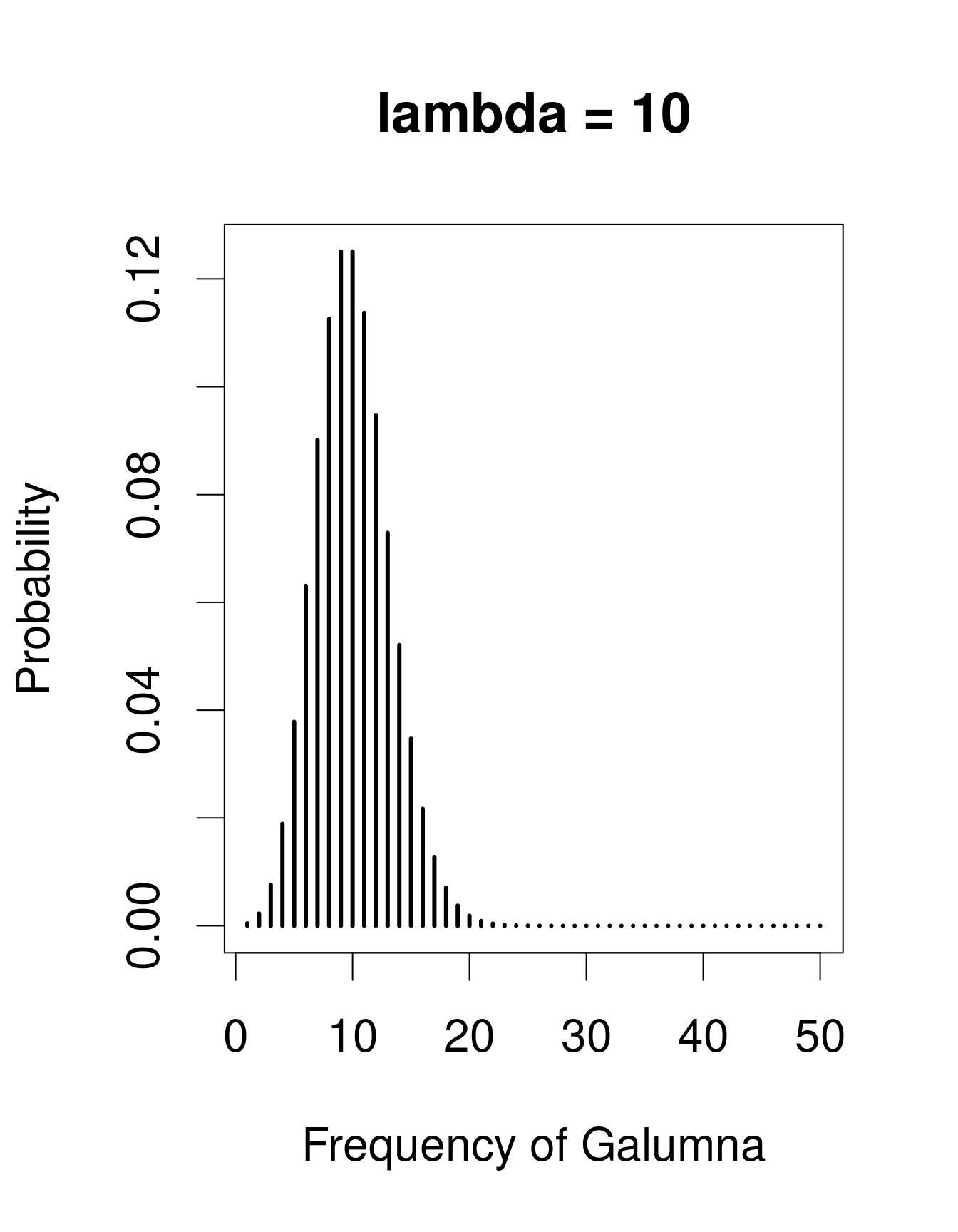
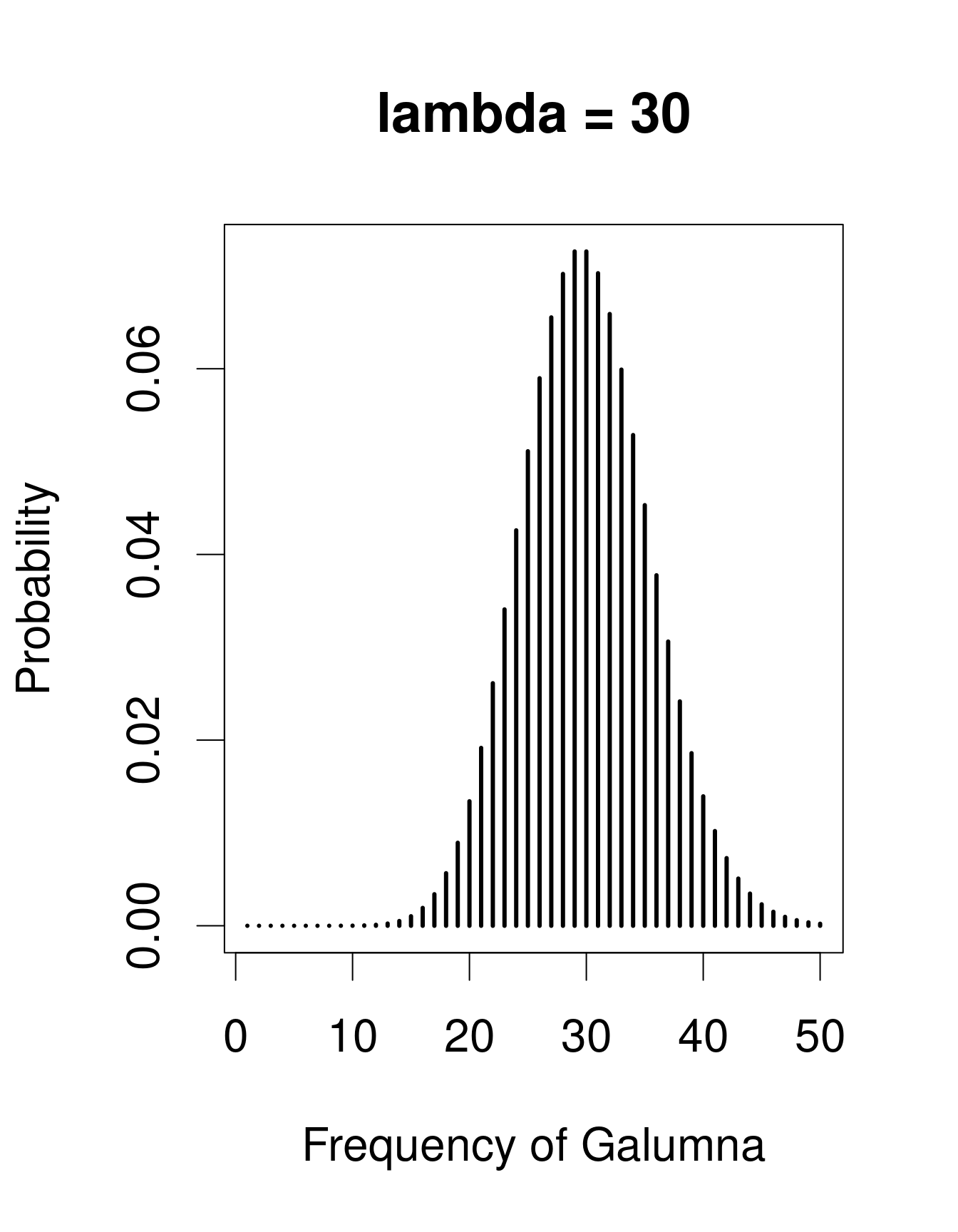
Remarquez que lorsque $\lambda$ est faible (c.-à-d. lorsque la moyenne s’approche de zéro), la distribution est décalée vers la gauche, alors que lorsque $\lambda$ est élevée, la distribution est symmétrique. La variance augmente aussi avec la moyenne (puisque les deux ont la même valeur), les valeurs prédites sont toujours des nombres entiers, et l’ensemble d’issus d’une loi de Poisson est strictement positif. Toutes ces propriétés sont utiles pour modéliser les données de dénombrement, p.ex. l’abondance d’un taxon, le nombre de graines dans une parcelle, etc. Notre variable mites Galumna semble suivre une loi de Poisson avec une basse valeur de $\lambda$ (en effet, si nous calculons l’abondance moyenne de Galumna pour l’ensemble des échantillons avec la fonction mean(), nous observons que cette valeur est proche de 0):

hist(mites$Galumna)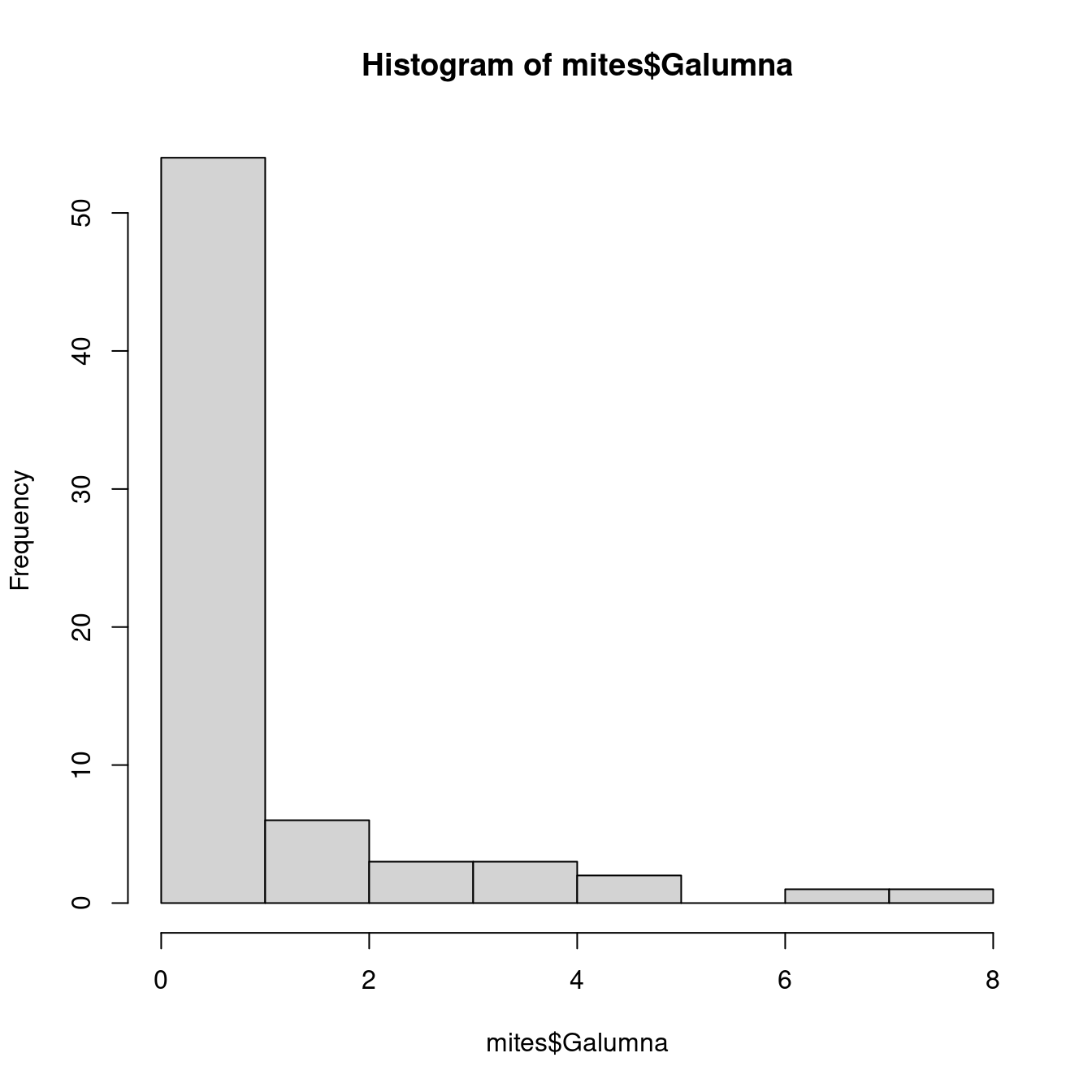

mean(mites$Galumna)

## [1] 0.9571429

La variable mites $pa (présence-absence) prend une autre forme. Cette variable n’inclut que des 0s et des 1s, de telle sorte que la loi de Poisson ne serait pas plus appropriée pour cette variable que la loi normale.

hist(mites$pa)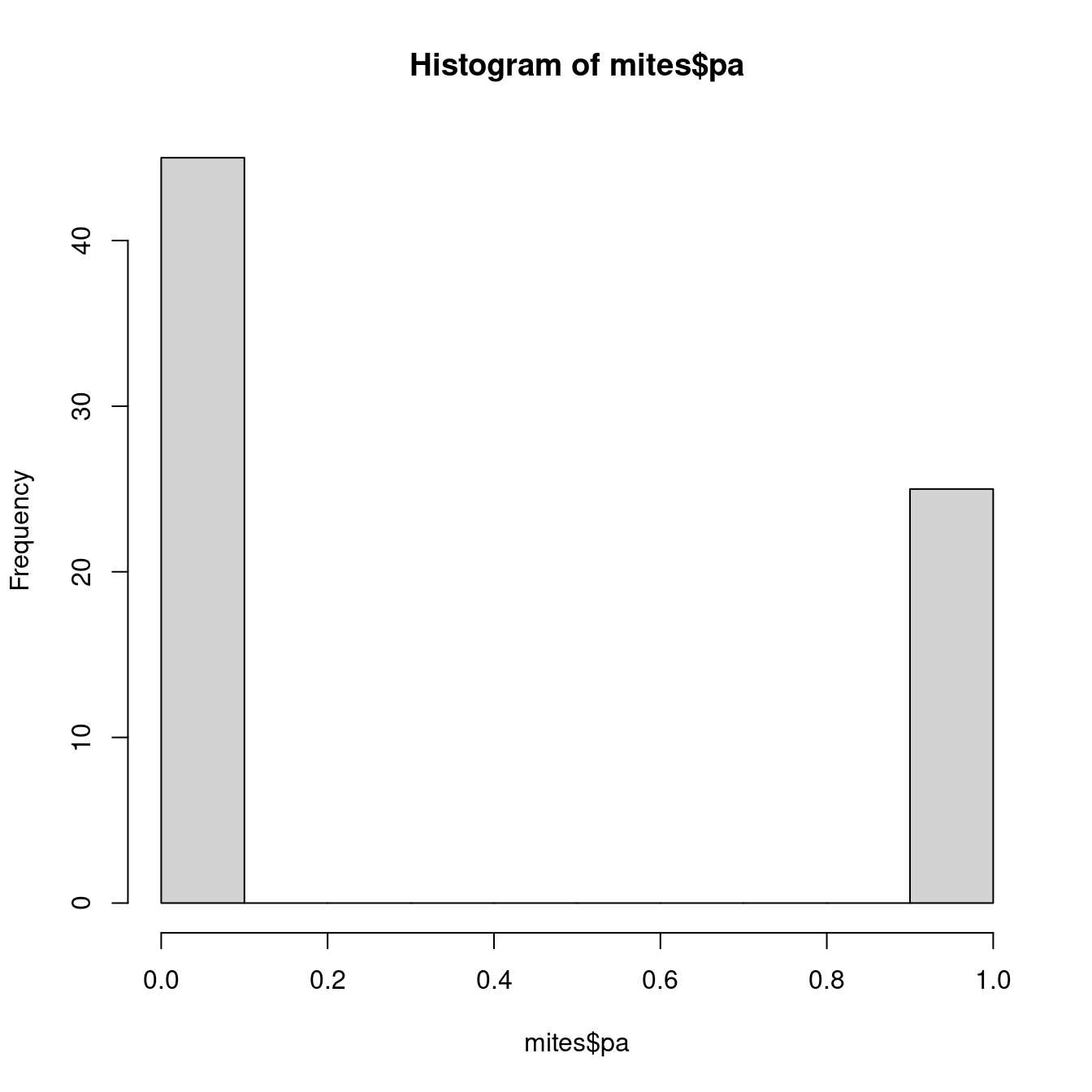

Nous avons besoin d’une distribution qui n’inclut dans son ensemble que deux issues possibles: 0 ou 1. La loi de «Bernoulli» est une distribution de la sorte. C’est souvent la première loi de probabilité qu’on nous présente dans les cours de statistiques, pour prédire la probabilité d’obtenir «pile» ou «face» en tirant à... pile ou face. Cette loi n’a qu’un paramètre: p, la probabilité de succès. Nous pouvons utiliser la loi de Bernouilli pour calculer la probabilité d’obtenir l’issue «Galumna présent» (1) vs. «Galumna absent» (0). Voici des exemples de distributions de Bernoulli avec différentes probabilités de présence ($p$):

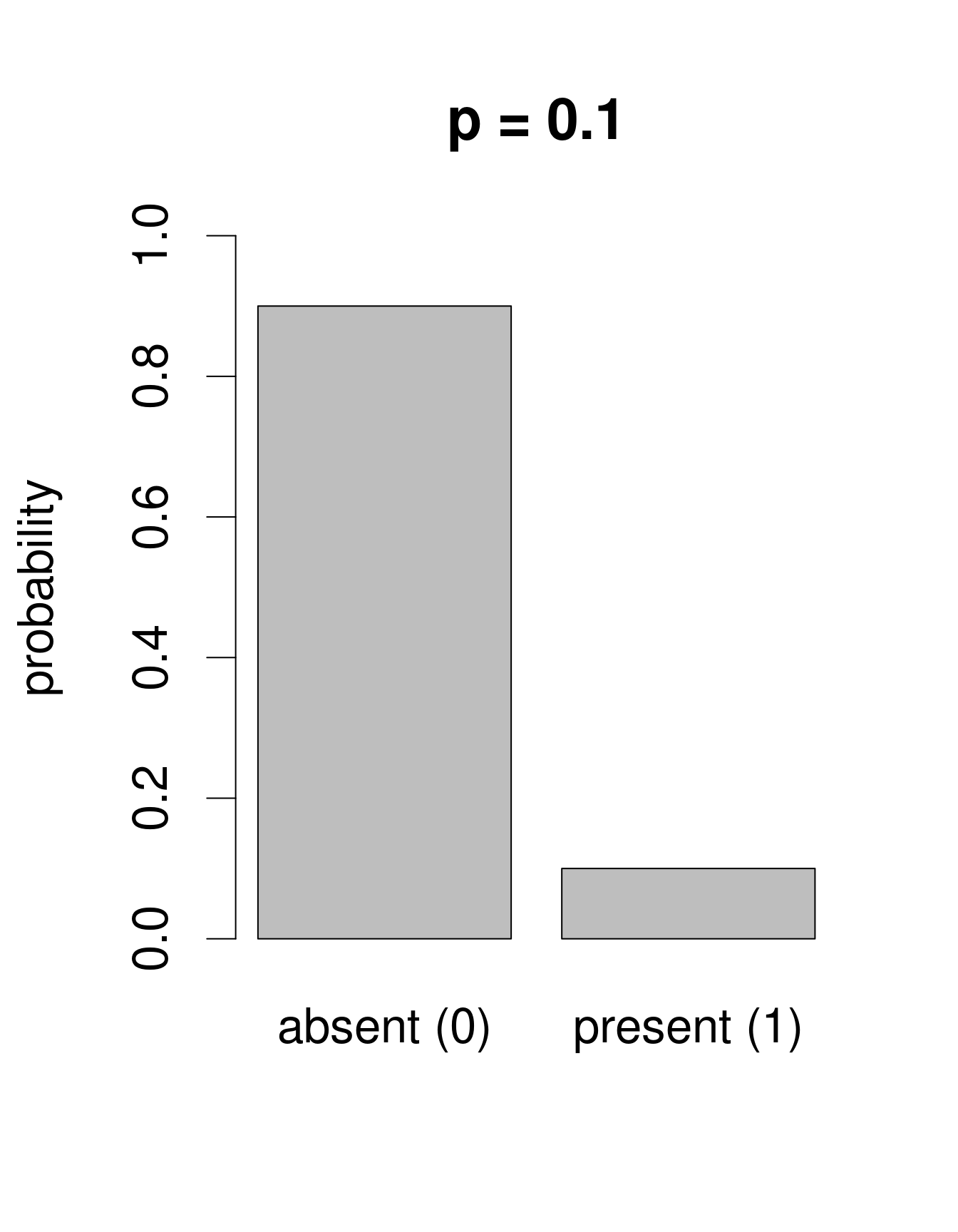
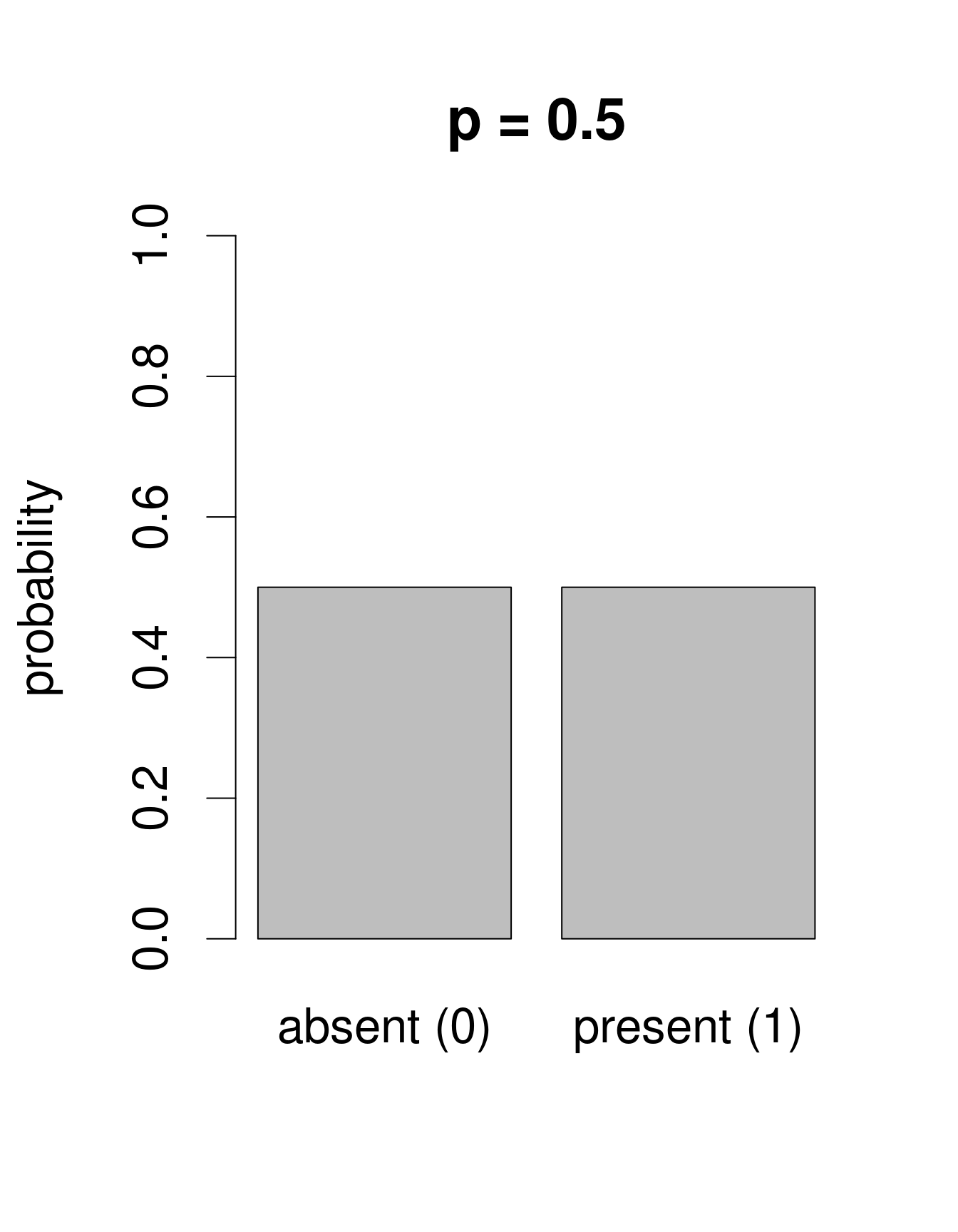
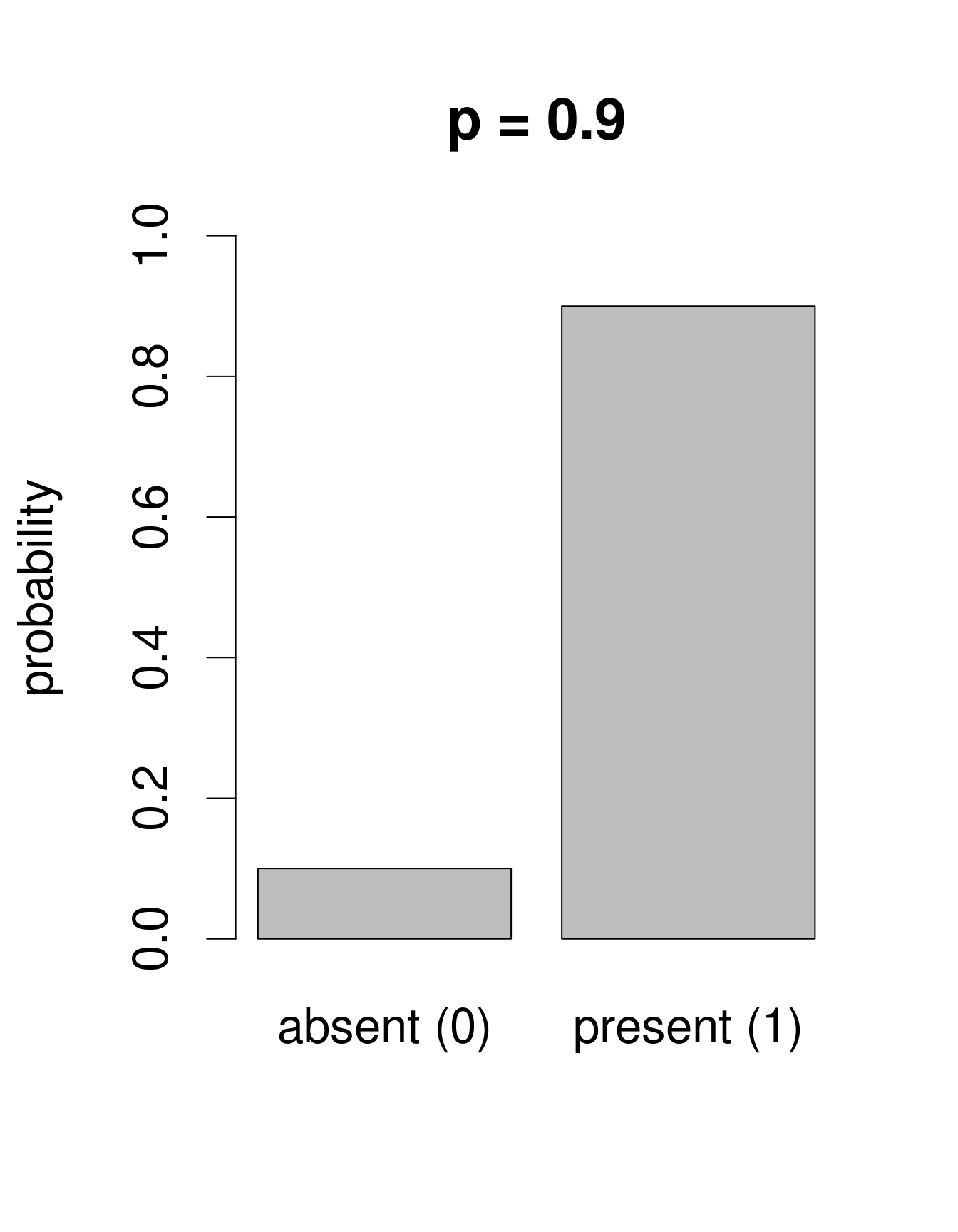
Nous pouvons calculer le nombre de sites où Galumna est présent par rapport au nombre total de sites pour obtenir un estimé de ce que $p$ pourrait être dans cet exemple:

sum(mites$pa)/nrow(mites)

## [1] 0.3571429

$p$ pour la variable mites ‘$pa’ est plus ou moins 0.36, de telle sorte qu’environ deux fois plus de sites montrent l’issu «Galumna absent
(0) que l’issu «Galumna présent» (1).

Lorsqu’il y a plusieurs épreuves (chacune avec un succès/échec), la loi de Bernoulli se transforme en loi binomiale, qui inclue le paramètre additionel $n$, le nombre d’épeuves. La loi binomiale prédit la probabilité d’observer une certaine proportion de succès, $p$, sur le nombre total d’épreuves, $n$. Un «succès» pourrait être, par exemple, la présence d’un taxon à un site (comme pour Galumna), le nombre d’individus qui survit pendant une année, etc. Voici des exemples de lois binomiales avec $n$ = 50 et trois valeurs différentes de $p$:

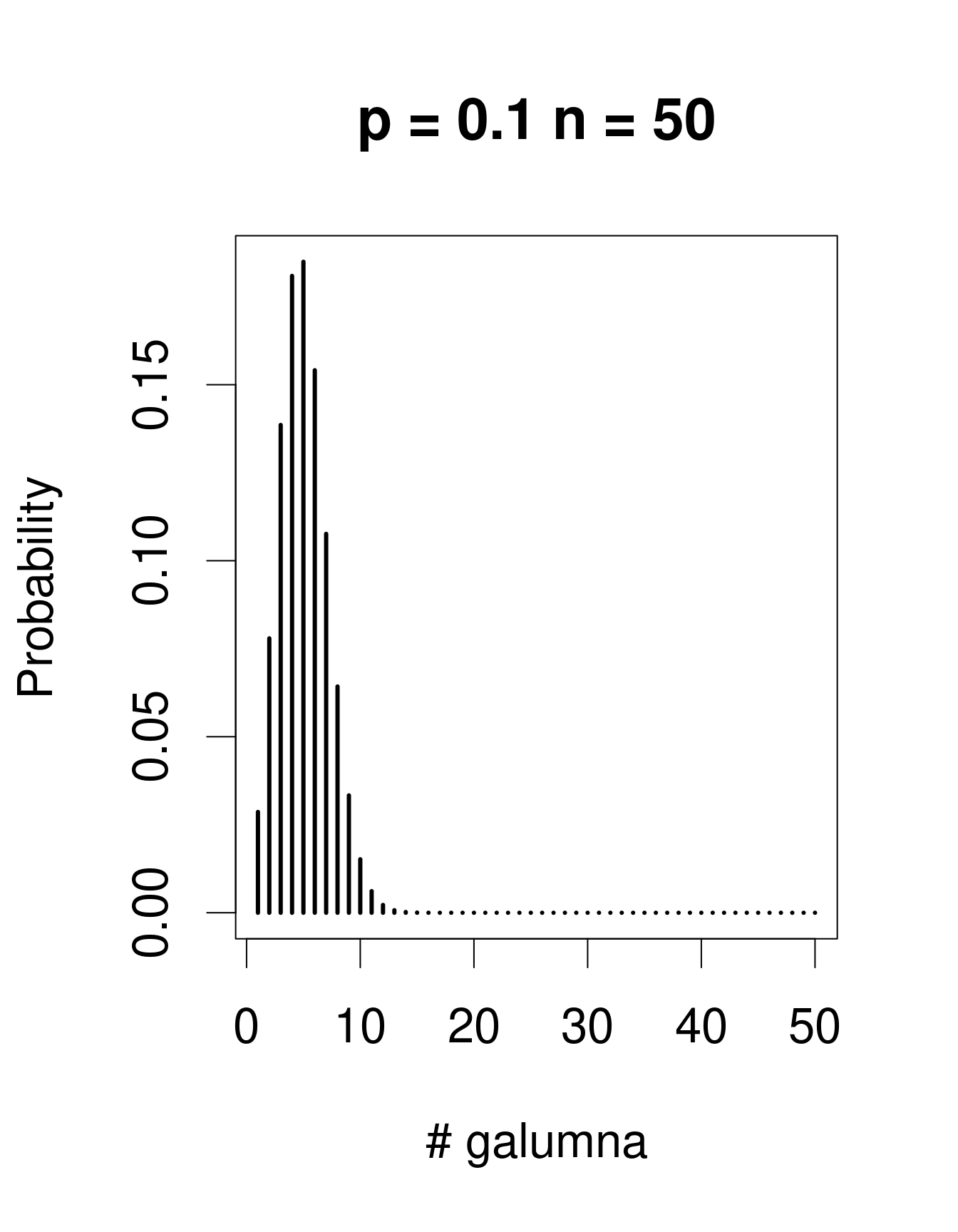
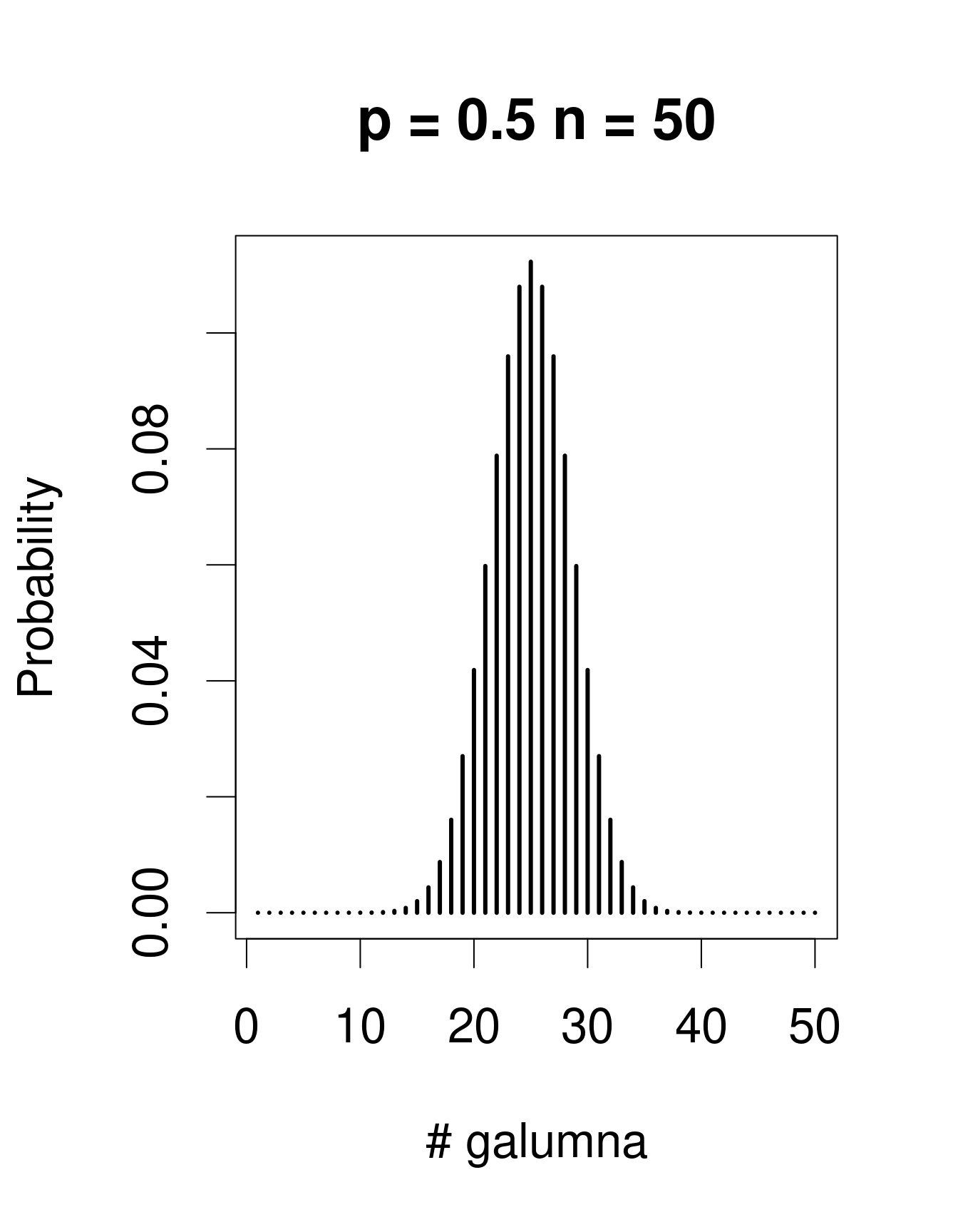
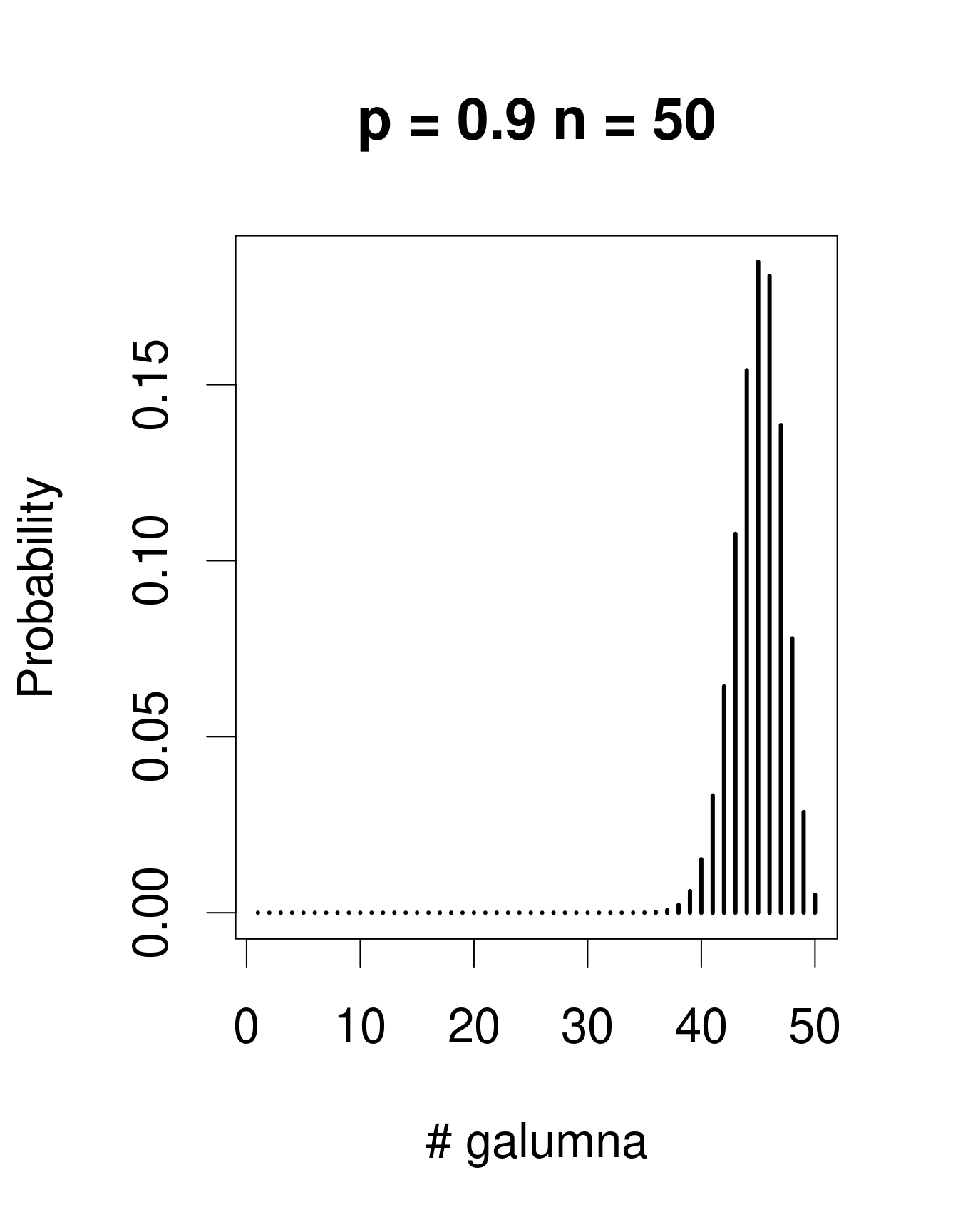
Remarquez que la loi binomiale est assymétrique et décalée à gauche lorsque $p$ est faible, mais elle est décalée à droite lorsque $p$ est élevé. C’est la différence principale avec la loi de Poisson: l’étendu de la loi binomial a une limite supérieure, correspondant à $n$. Conséquemment, la loi binomiale est utilisée pour modéliser des données lorsque le nombre de succès est donné par un nombre entier, et lorsque le nombre d’épreuves est connu. Nous pouvons utiliser la distribution binomiale pour modéliser nos données de proportion, où chaque mite échantillonée pourrait être considérée comme une épreuve. Si la mite est du genre Galumna, l’épreuve est un succès (1), sinon, c’est un échec (0). Dans ce cas, le nombre d’épreuves $n$ varie pour nos 70 échantillons selon l’abondance totale de mites dans l’échantillon, alors que $p$, la probabilité de succès, est donné par la proportion de Galumna dans chaque échantillon.

Pourquoi tout cette discussion à propos des lois de distribution? Parce que n’importe quelle loi peut être utilisée pour remplacer la loi normale lorsqu’on calcule les valeurs estimées dans un modèle linéaire. Par exemple, nous pouvons utiliser la loi de Poisson pour modéliser nos valeurs d’abondance en utilisant l’équation suivante:

\[Y_i \sim Poisson(\lambda = \beta_0 + \beta_1X_i)\]

Remarquez que $\lambda$ varie selon $x$ (contenu d’eau), ce qui signifie que la variance dans les résidus variera aussi selon $x$ (car pour la loi de Poisson variance = aussi $\lambda$). Ceci veut dire que nous venons de nous défaire de la supposition d’homogénéité de la variance! Aussi, les valeurs estimées seront désormais des nombres entiers plutôt que des nombres décimaux car ils seront tirés de lois de Poisson avec différentes valeurs de $\lambda$. Ce modèle ne prédiera jamais de valeurs négatives car l’ensemble d’une loi de Poisson est toujours strictement positif. En changeant la distribution des résidus ($\varepsilon$) de normale à Poisson, nous avons corrigé presque tous les problèmes de notre modèle linéaire pour l’abondance de Galumna.

Ce modèle est presque un GLM de Poisson, qui ressemble à ça:

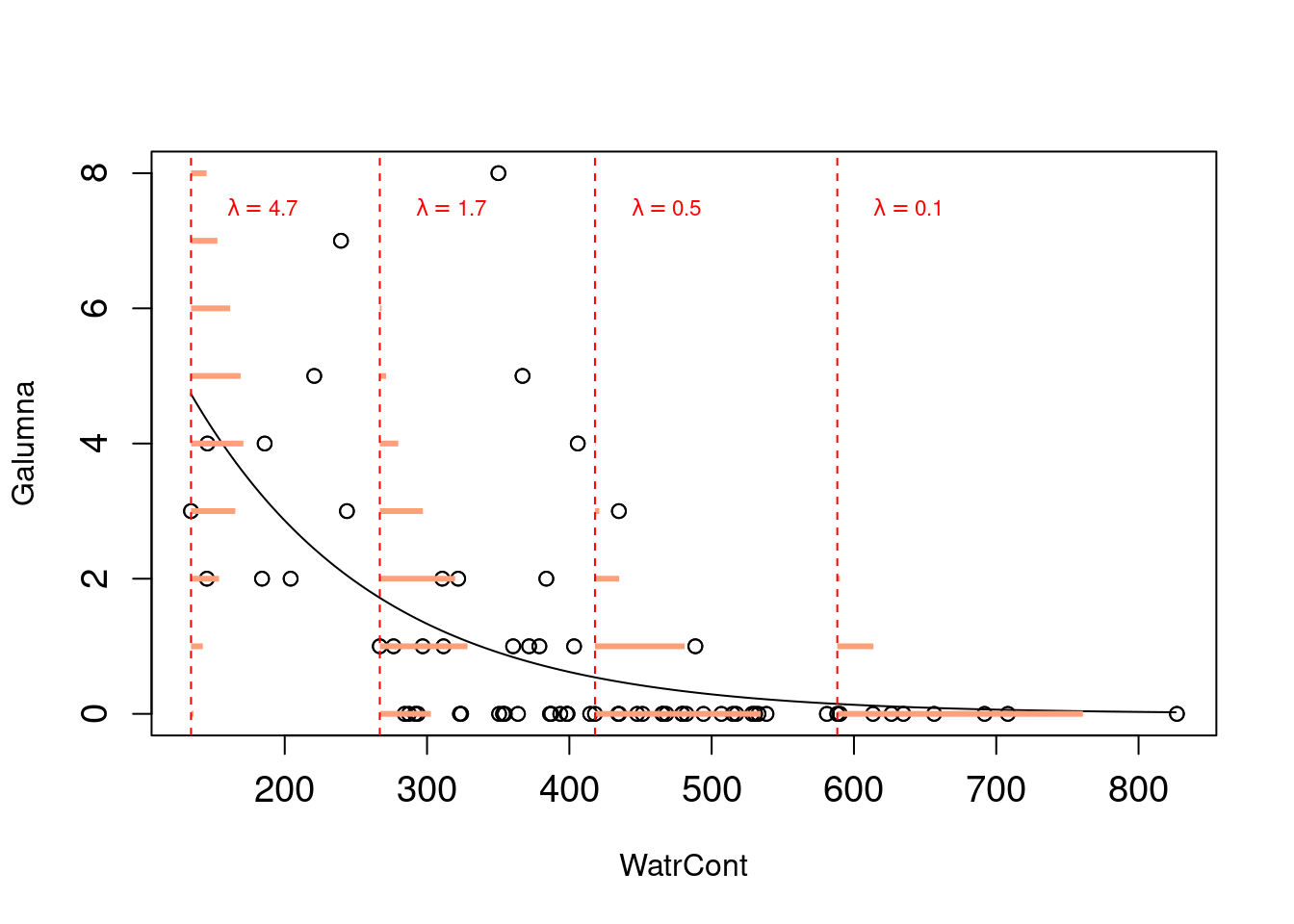
Remarquez que les probabilités d’observer différentes valeurs estimées (en orange) sont maintenant des nombres entiers, et qu’autant la variance que la moyenne de la distribution declinent lorsque $\lambda$ diminue avec le contenu d’eau. Pourquoi la droite de régression est-elle courbée? Pourquoi est-ce que ce modèle se nomme un «modèle linéaire généralisé»? Continuez votre lecture!